- 1. introduction
- 2. Multimode fiber imaging
- 3. real time terahertz beamforming
- 4. random spectrometry
- 5. non-Hermitian physics
- 6. Conclusion and future work
- 7. List of publications
- 8. Interesting things
Date: 2:30 pm, Feb 8 2024.
Thesis Committe:
1. introduction
Hello everyone!

My phd thesis is about the use of machine learning methods in physics research.
First I will give an introduction on AI, machine learning and related stuff.
Then I will use four examples to talk about applications of machine learning in different aspects in physics from MMF image reconstruction to non-Hermitian physics.
At the end, I will provide a conclusion and talk about future implications.

Since 1950s, artifical intelligence has been developed for nearly 70 years. However, it is until recent decades that AI starts to attract people’s attention, especially with the coming of large AI models. For example, in 2016 AI model Alpha Go was proved to beat world no.1 go player. In last year, chatgpt has shown the ability to do conversations like a normal human being.
Given the big achievement made by AI models, we as physicist would naturally think: Can we use AI in physics?
Yes, that’s exactly what I am doing here.

Since the begining of my research, I have been thinking about the following three questions:
First, What advantage does AI have compared to conventional methods?
Can our knowledge from physics systems guides the explanation of AI models?
And What are the challenges and obstacles while applying AI in physics?
Throughtout this presentation, I will try to answer these questions. However, one thing to note is AI is still under rapid development, no one is able to predict what will happen in the future. Therefore, I will focus on provide answers based on my current understanding.
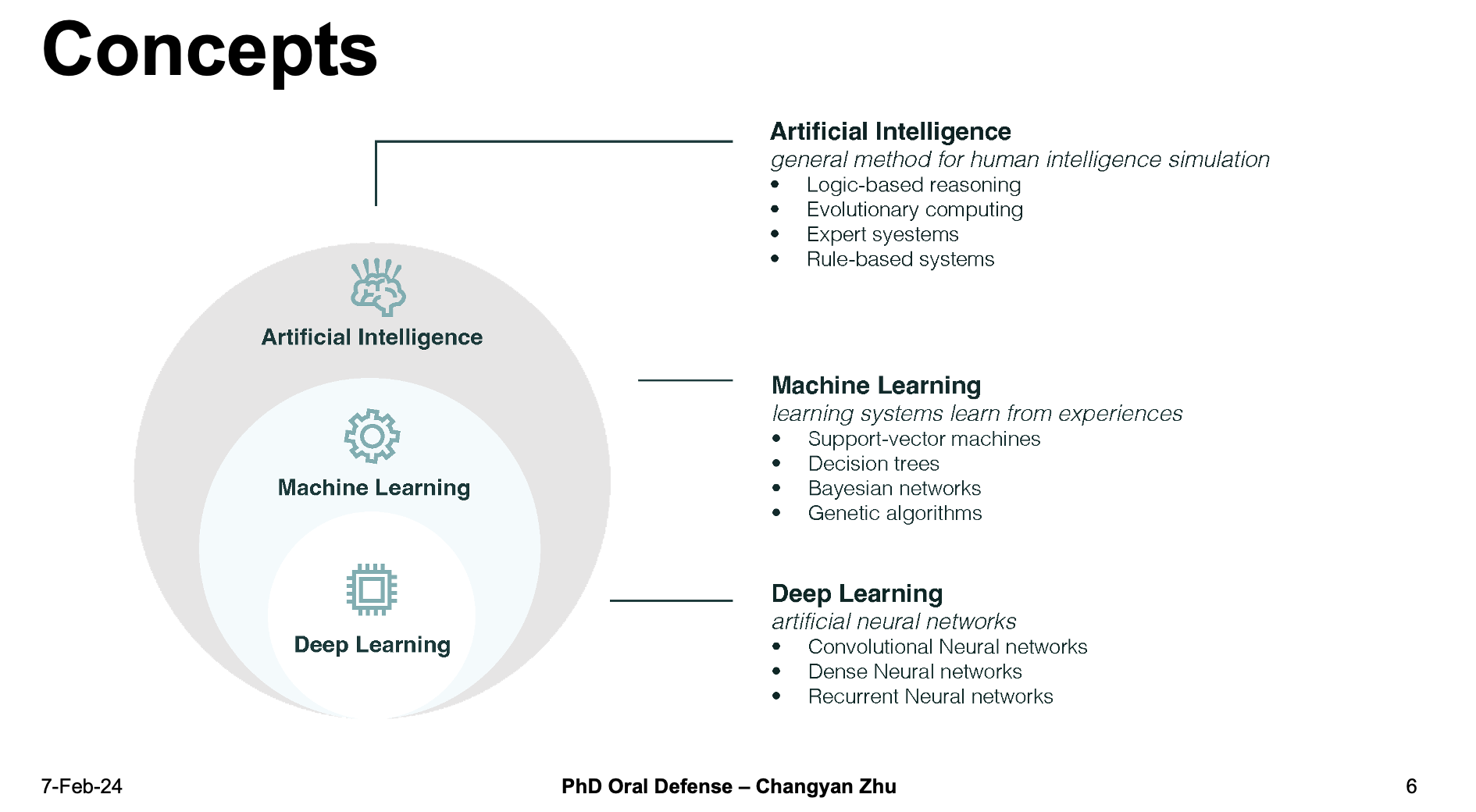
Firstly , I felt that there is a need to distinguish the following three concepts.
- AI, or artificial intelligience, is a general method for human intelligence simulation, includes a broad range of topics from logical-based reasoning to expert systems.
- As a part of AI, machine learning focuses on learning systems learned from experiences, e.g.., models that are trained on datasets.
- Deep learning, as a subfield of machine learning, focuses on the use of artificial neural networks with representation learning.
Since most of the current AI models are machine learning especially deep learning models, my research is carried on mostly based on machine learning methods.
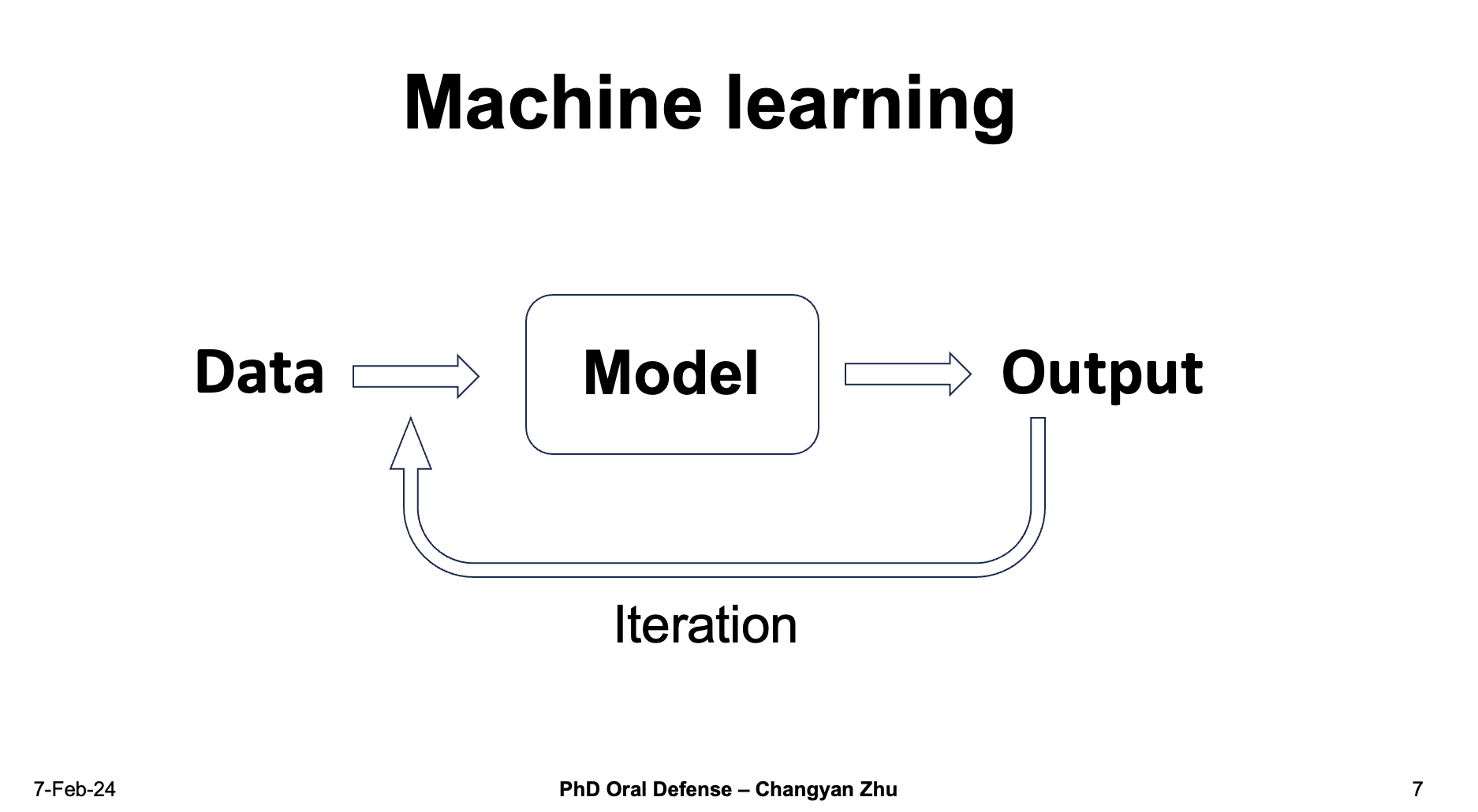
A general scheme for machine learning include a model that can learn from data input and predict the output. The output is iteratively compared with the dataset and update the model parameters. This is different from what we see things in physics.
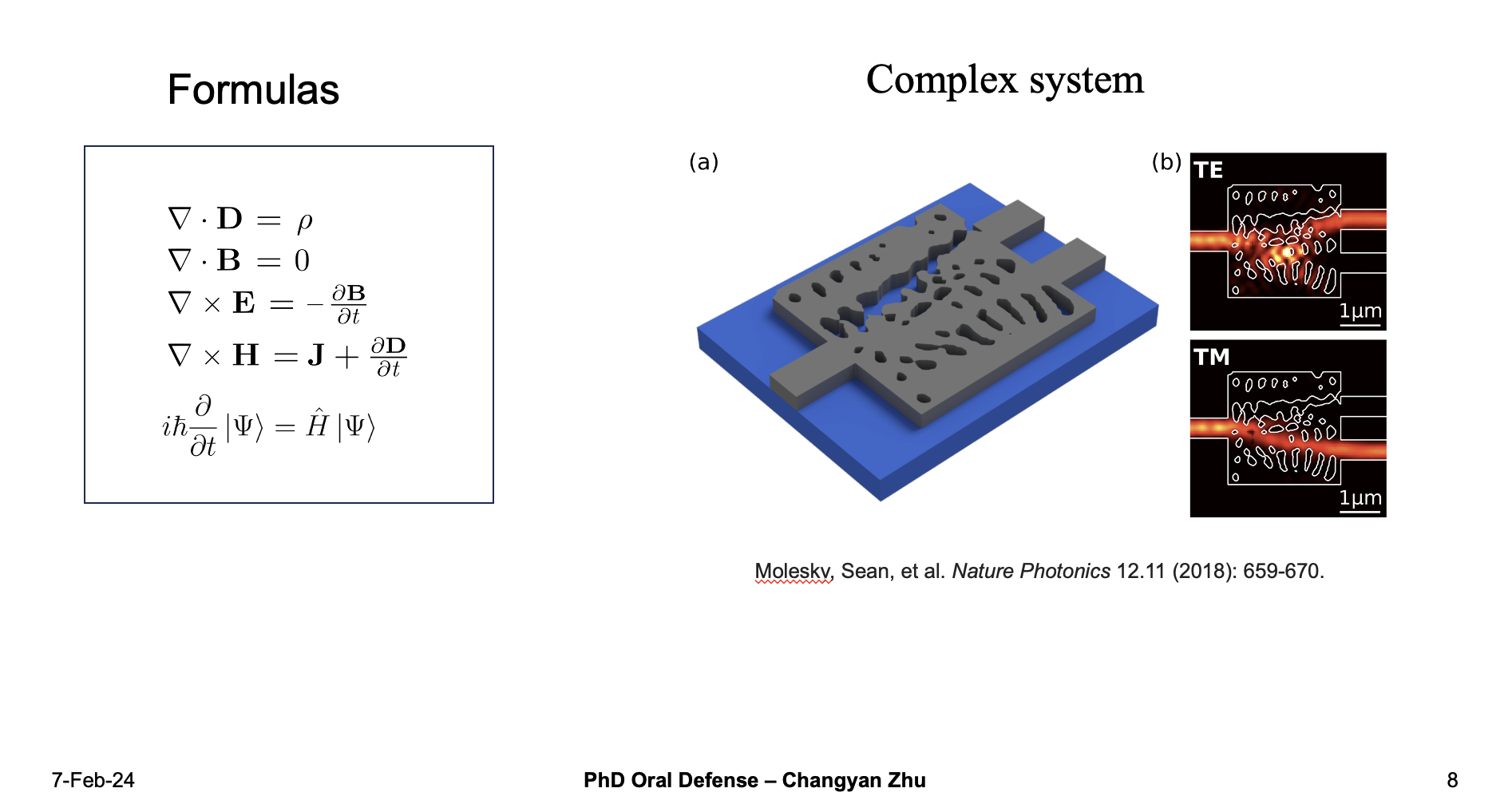
What kind of physics system needs AI?
In physics, we tend to use formulas to describe everything. For example, with Maxwelll equations you can understand the behaviours of electromagnetic fields, with Schrodinger equation you can know the behaviour of a quantum system.
However, when the systems go very complex, for example if you have a inverse design problem in photonic area, although in principle you can use FDTD simulation to solve the maxwell equations and get the results, one forward simulation usually takes up to several hours or even up to several days. In this situation, machine learning can be used to approximate the structure and give a quick prediction in much time.
So how does machine learning models look like?
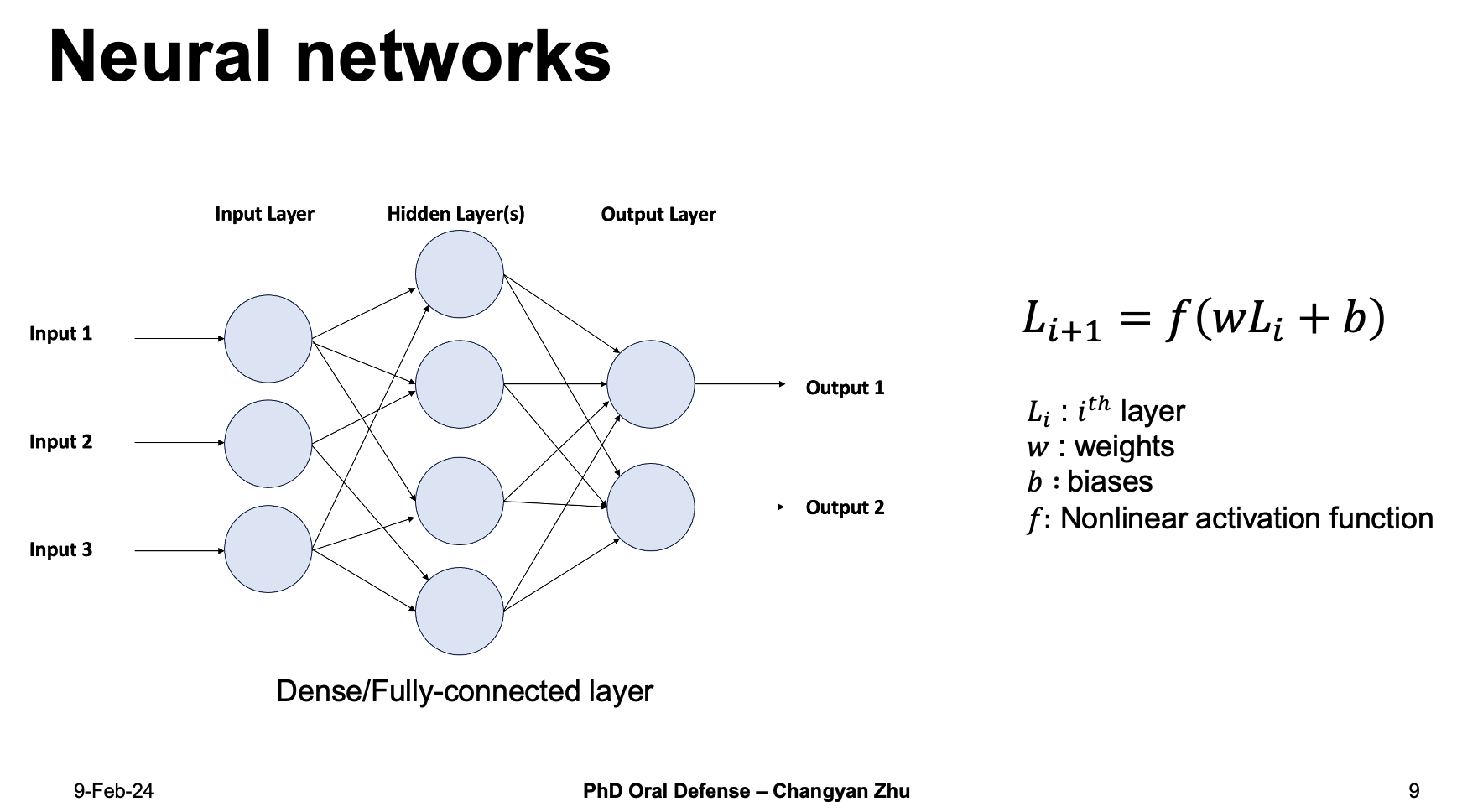
A general neural network usually consists of several parts including input, output and hidden layers. The data is transmitted between the layers with a nonlinear function f(wL+b), w and b are called weights and biases, during the training processes they will be updated. The nonlinear activation function is used to ensure a nonlinear relationship that can be used to simulate complex problems.
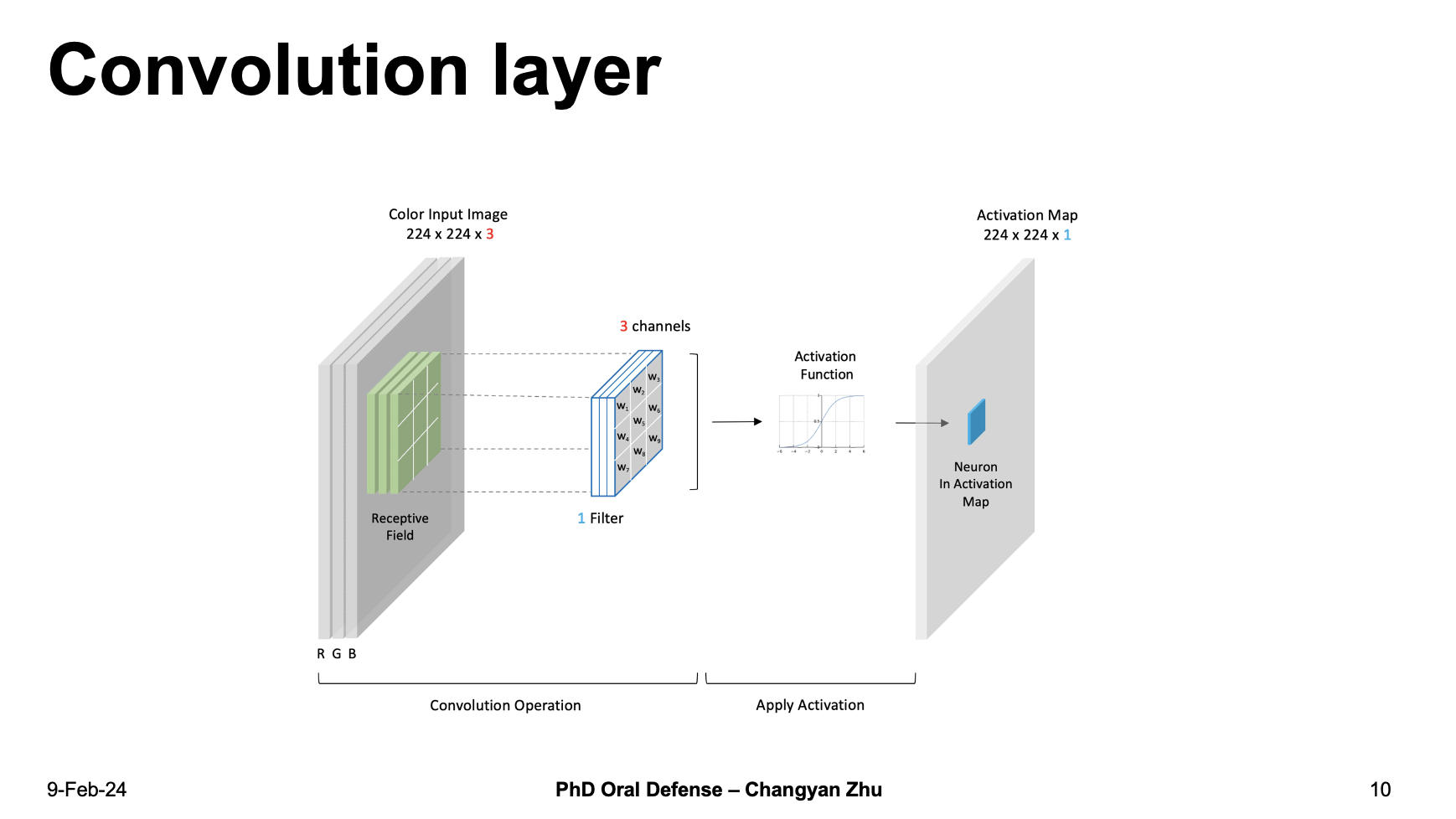
Compared to dense layers, we also have convolutional layers that are inspired from human vision process. For example, when you are trying to look at a image, your eyes are automatically scanning through the image, similar to this, convolutional layer use a kernel matrix to scan through the input image and extract the feature from images. Since convolution layers are inspird from human vision, they are often considered as better at handling image relatead problems.
2. Multimode fiber imaging
Now we have introduced two different kinds of neural networks and show that they can be used to approximate complex systems. Let’s look at a first example, multimode fibers.
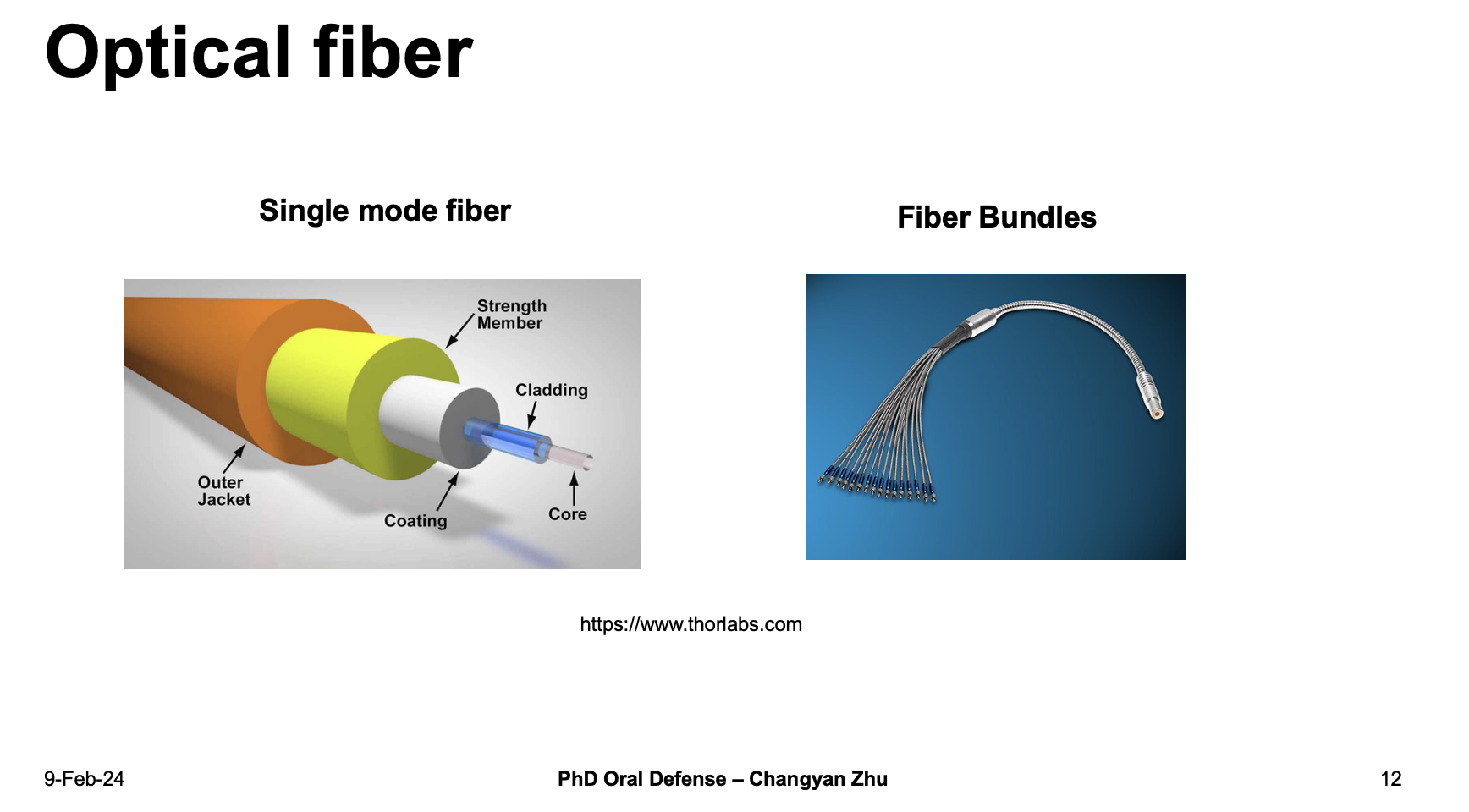
Optical fibers are widely used in data transmission and endoscopy, most of our lab computers and large linux servers are using fibers to communicate. Actually, most of the fibers we are using are called single mode fibers, which can hold one mode in a fiber core. Therefore, if we want to increase the fiber bandwidth, we need to combines a lot of single fibers together and make a fiber bundle.
However, the size of the fiber bundles set a limitation for fiber transmission. How can we overcome this?
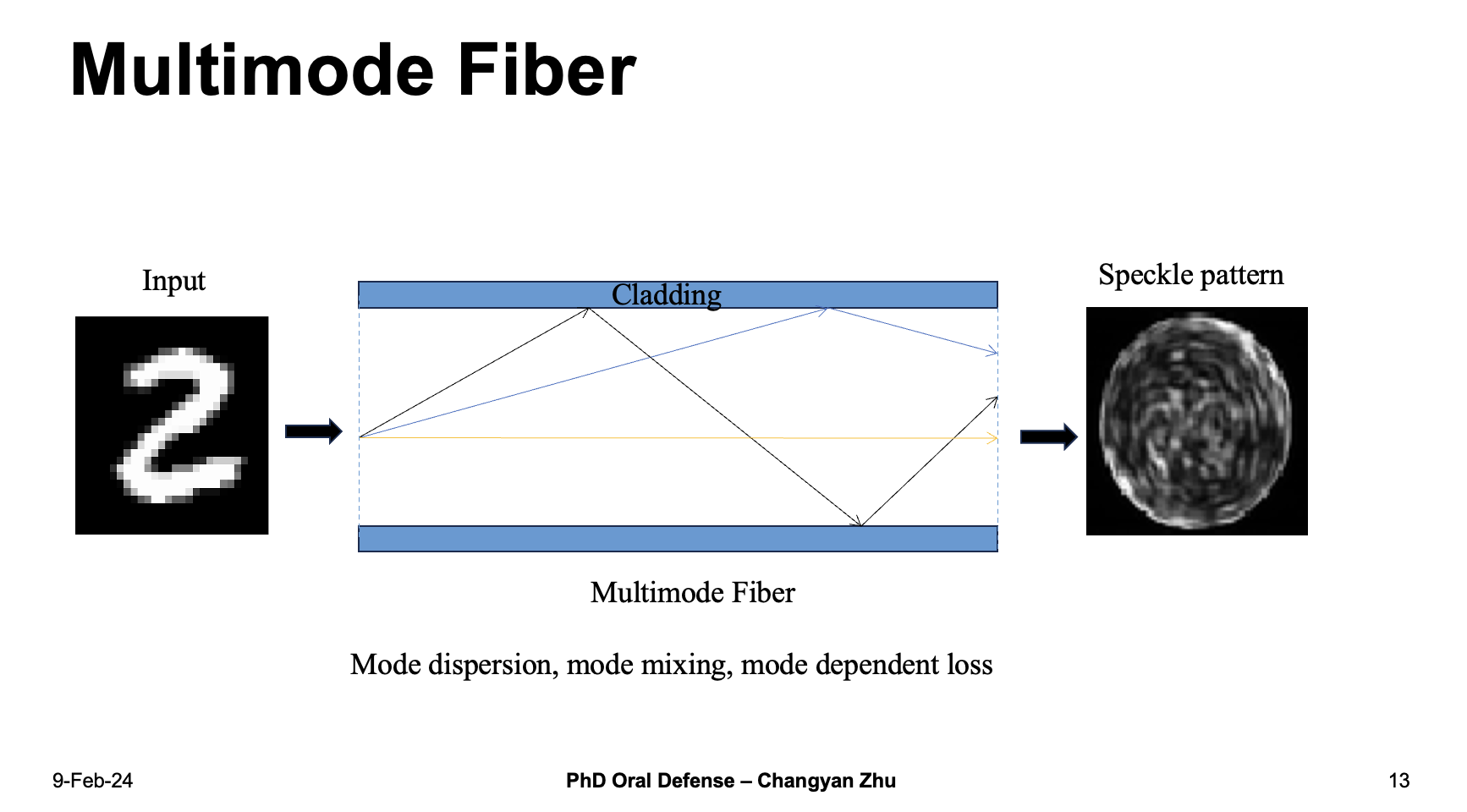
The solution is to use a multimode fiber which has a larger core diameter and can hold hundreds or thousands of modes inside a single fiber. However, MMFs also have their own drawbacks, different modes propagates inside the MMF in a different phase velocities, together with mode mixing and mode dependent loss, create a seemingly random speckle pattern at the end.
To recogize the ground truth image from the speckle pattern requires a lot of effort. One of the way is extract the phase information by adding a reference beam in the optical setup.
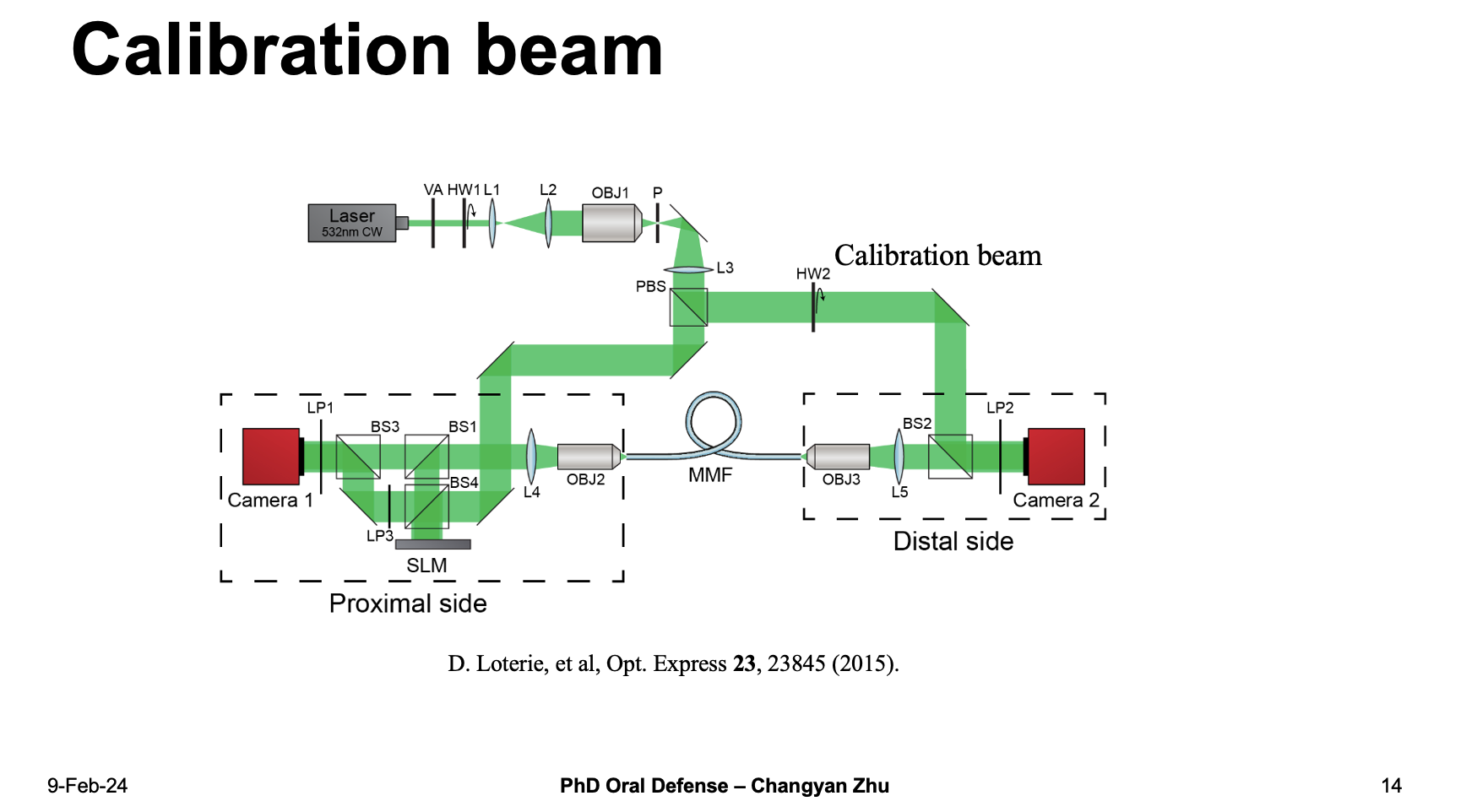
The added calibration beam use inteference to obtain the phase information. However, in actual applications such as endoscopy it is actually very hard to have a reference beam. So, can we do MMF image reconstruction with a intensity-only detection?
The answer is yes. With the help of machine learning, we will show that it is possible to transmit signals with intensity only detections.
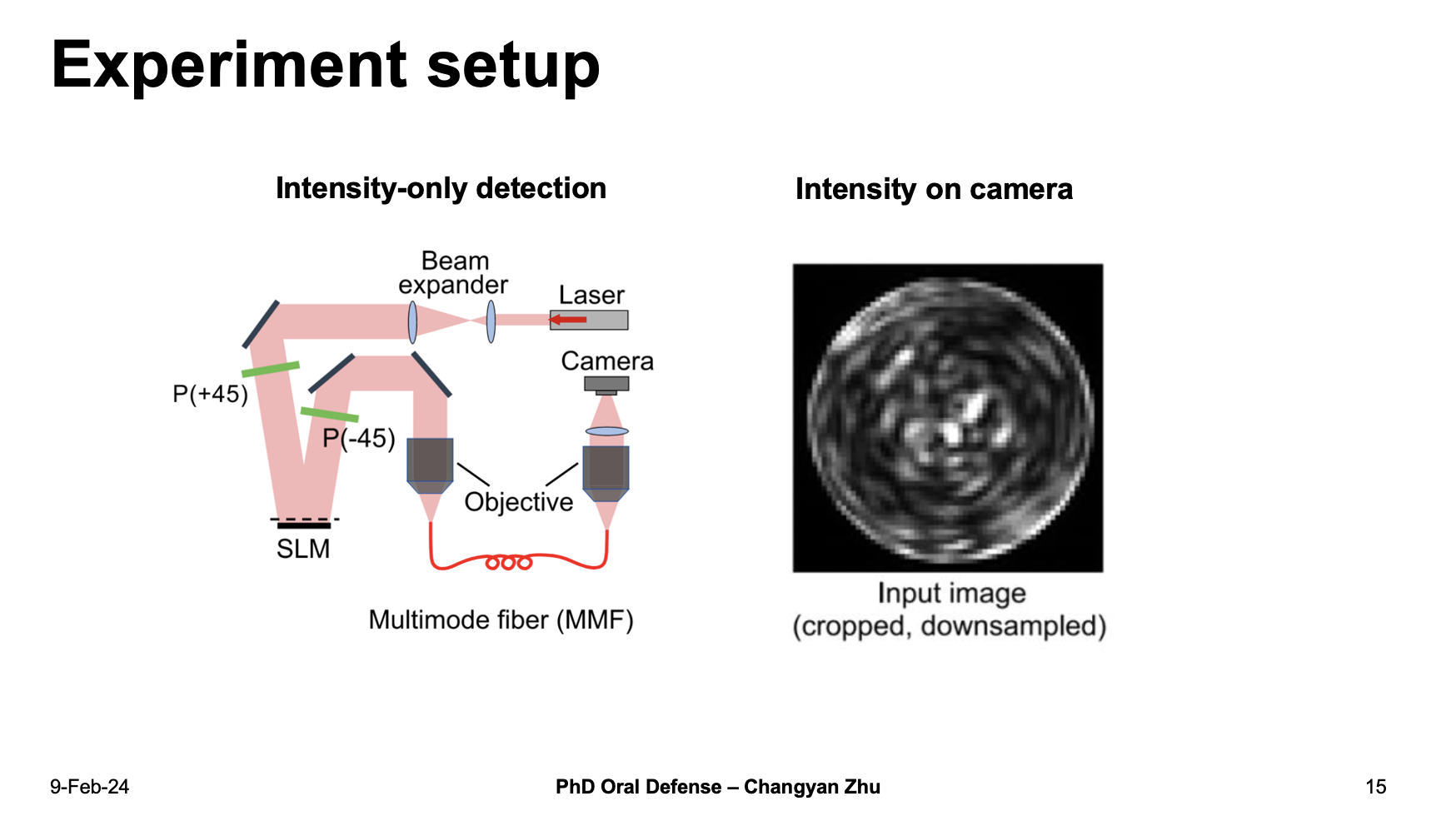
Here is the experiment setup. You can see that only one camera is used to measure the intensity information, as shown in the right figure.
The speckle pattern together with input images are send to neural networks for training.
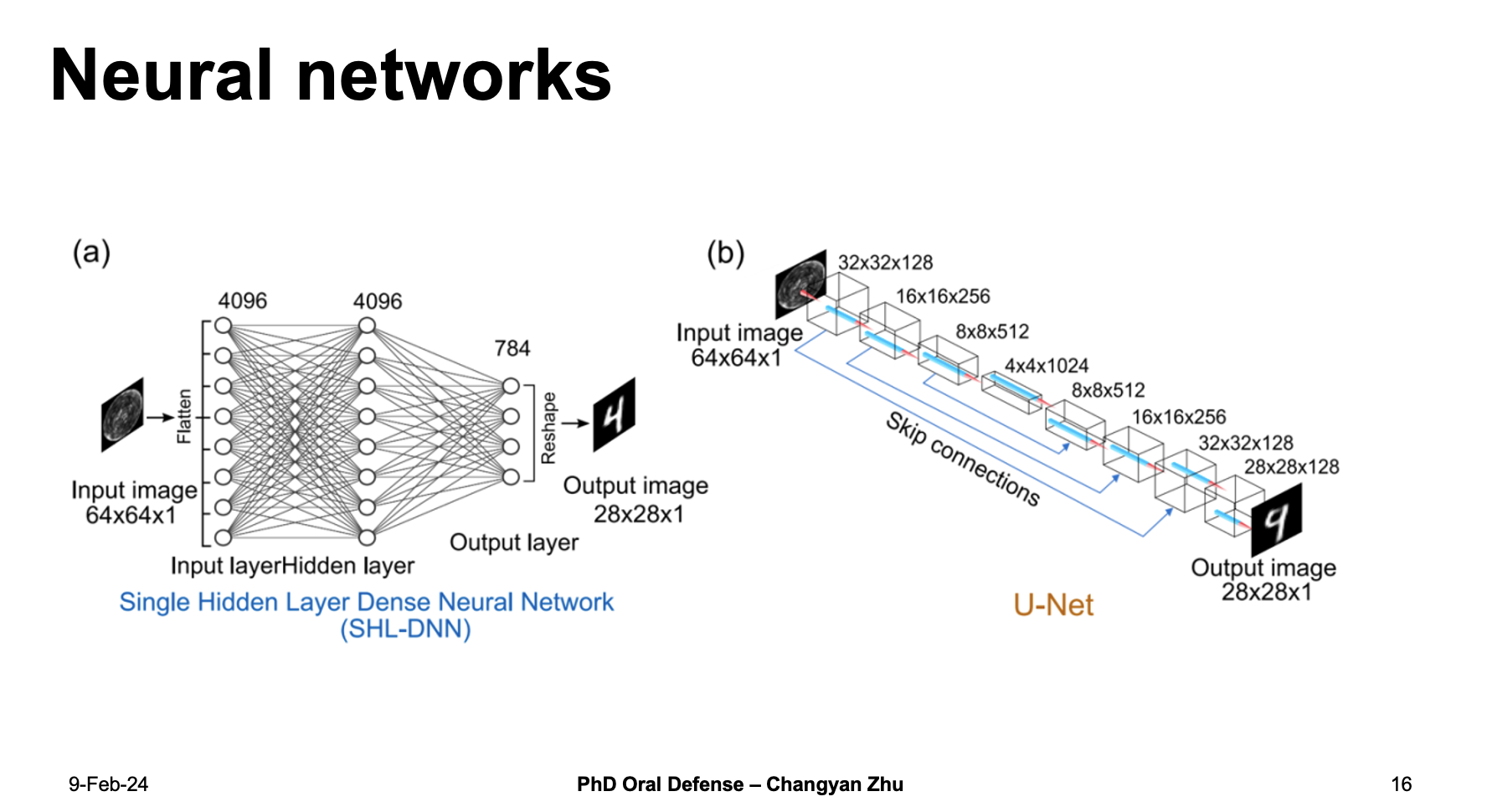
For the neural network, we choose two different kind of neural network to do a comparison. The first is SHL-DNN which uses dense layers, a single hidden layer is used between the input and output layers. For comparison, we choose U-net which consists of several layers of convolution layers. After training, the results for the test datasets are shown here.
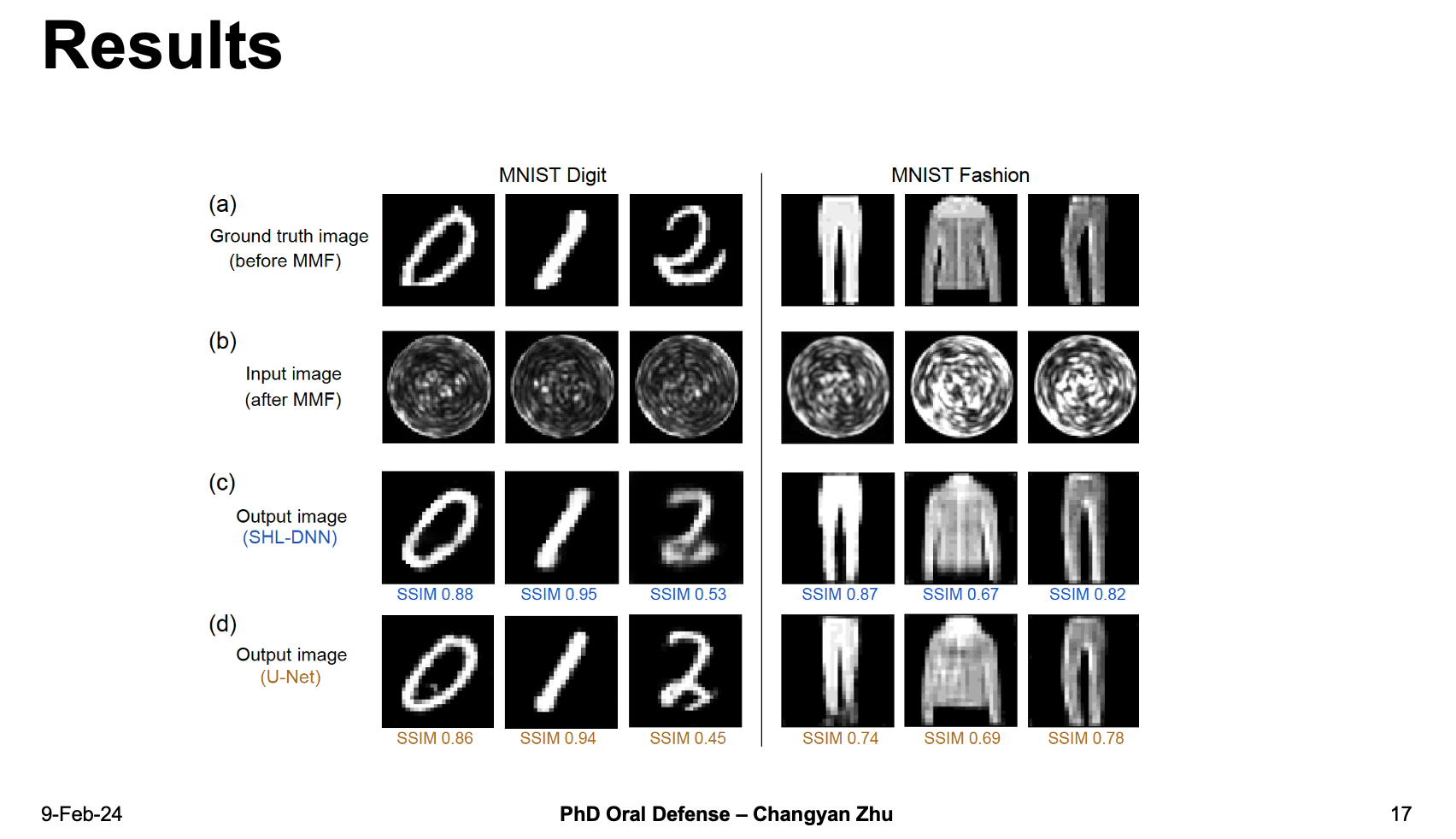
The first line are the ground truth images and second line are speckle patterns. As you can see, both SHL-DNN and U-net give pretty good reconstruction results compared to the ground truth images, both for MNIST digital dataset and MNSIT Fashion dataset. We also use SSIM value to quantify how similar the reconstructed images are compared to ground truth images.
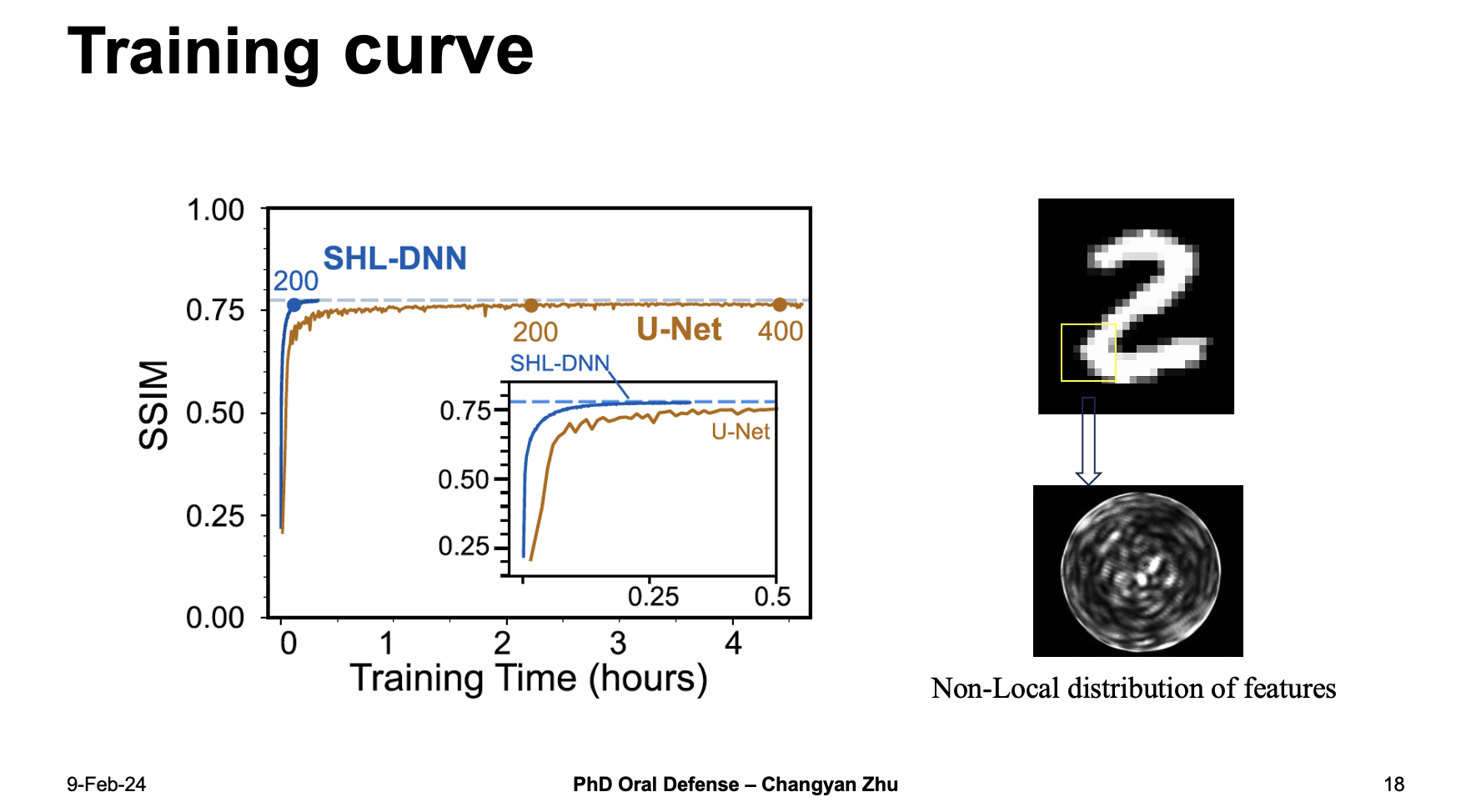
Take a look at the training curve, you can see that as the training time goes up, the SSIM value of SHL-DNN goes up very quickly and finally reaches a large value of above 0.75, while the U-net takes a much longer time and finally reach a similar results.
Why does SHL-DNN outperforms U-net desipte the fact that U-net are more accepted in image processing? One possible explanation is about the non-local distributions of speckle pattern features. When the local features of a input are inputed into a MMF, the local features will become globally distributed because of the mode dispersion inside the MMF. Since the dense layer are utilizing all the information in the speckle patterns, it can give a better prediction of the ground truth images.

We also want to know whether machine learning is learning the physical properties of MMF or it is just learning a map between input and output data, therefore, we design a dataset without digit 9 and use it to train a neural network model. Suprisingly both neural networks are able to reconstruct digit 9 even the dataset doesn’t include any digit 9. This demonstrate teh transfer learning ability of machine learing methods.

In MMF applications, temperature variations are often considered as an important factor to avoid, hence we design a temperature perturbation test by control the MMF temperature from 25 to 75 degrees. Using a dataset collected from 25 degress to train a neural network and then use it to reconstruct the speckle pattern at different temperatures.

For the MNIST dataset, the machine learning model gives pretty good results even the temperature goes up to 75 degrees. For the ImageNet dataset which uses natural images as the MMF input, although the reconstruction fidelity is lower than the original image, the truth that neural networks can perform MMF image reconstruction at 75 degree already shows machine learning can help overcome temperature variations in MMFs.
3. real time terahertz beamforming
Now we have shown that machine learning can achieve high fidelity image reconstruction in MMFs, which can be used in lab computers or large servers. But actually most of our daily used devices such as cell phones or labtops are using wiredless communication techniques such as 5G networks.
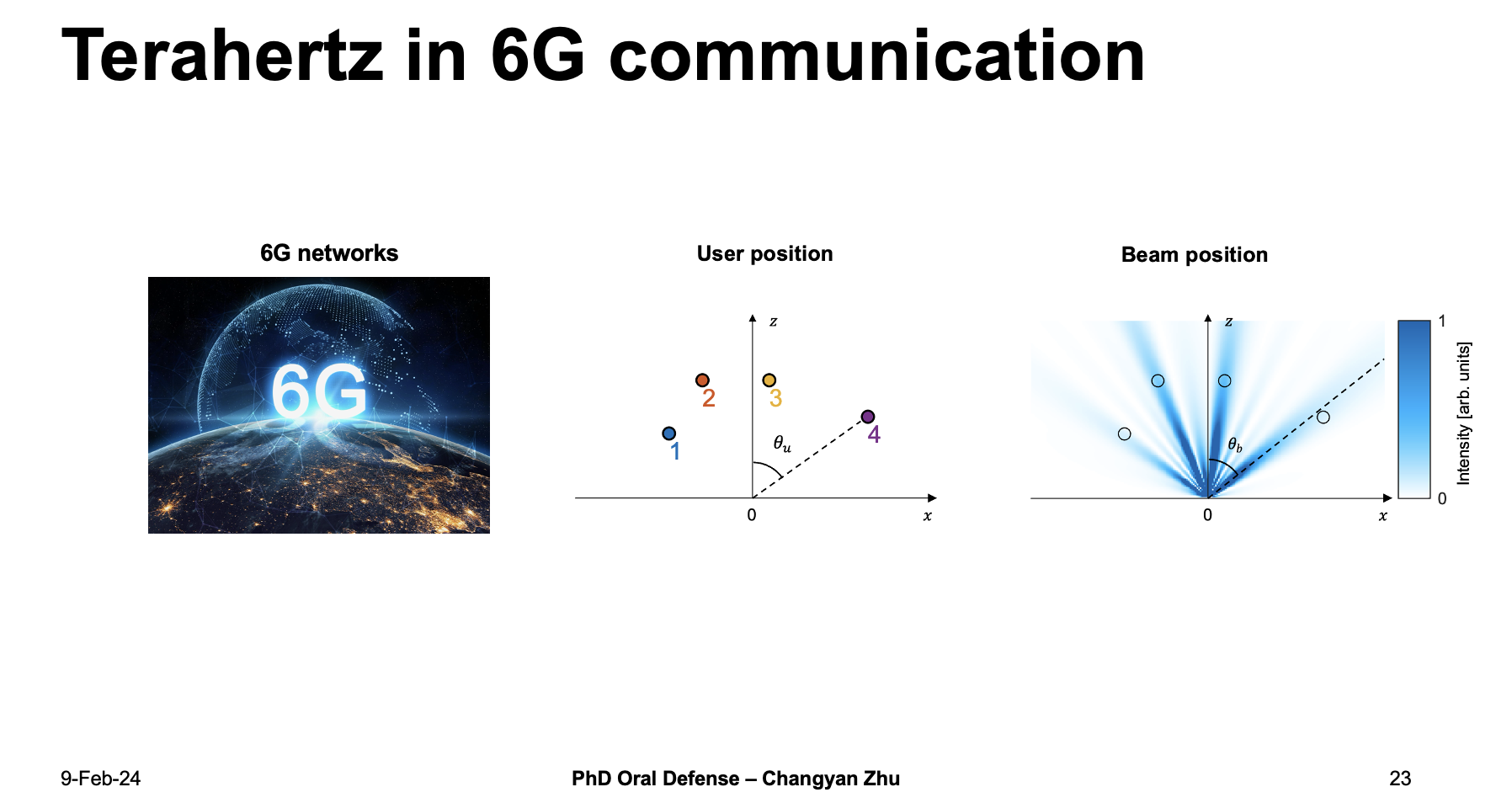
The next generation of 5G is called 6G, which requires high transmission rate and quick data responce. To achieve this, terahertz become a very strong candidate because it holds a large bandwidth. However, the spectral effciency need to be improved because THz beam has a relatively small beam width.
For example, if we have four users here, only if the beam positions are located at the user poitions that the spectral effciency is maxmized.
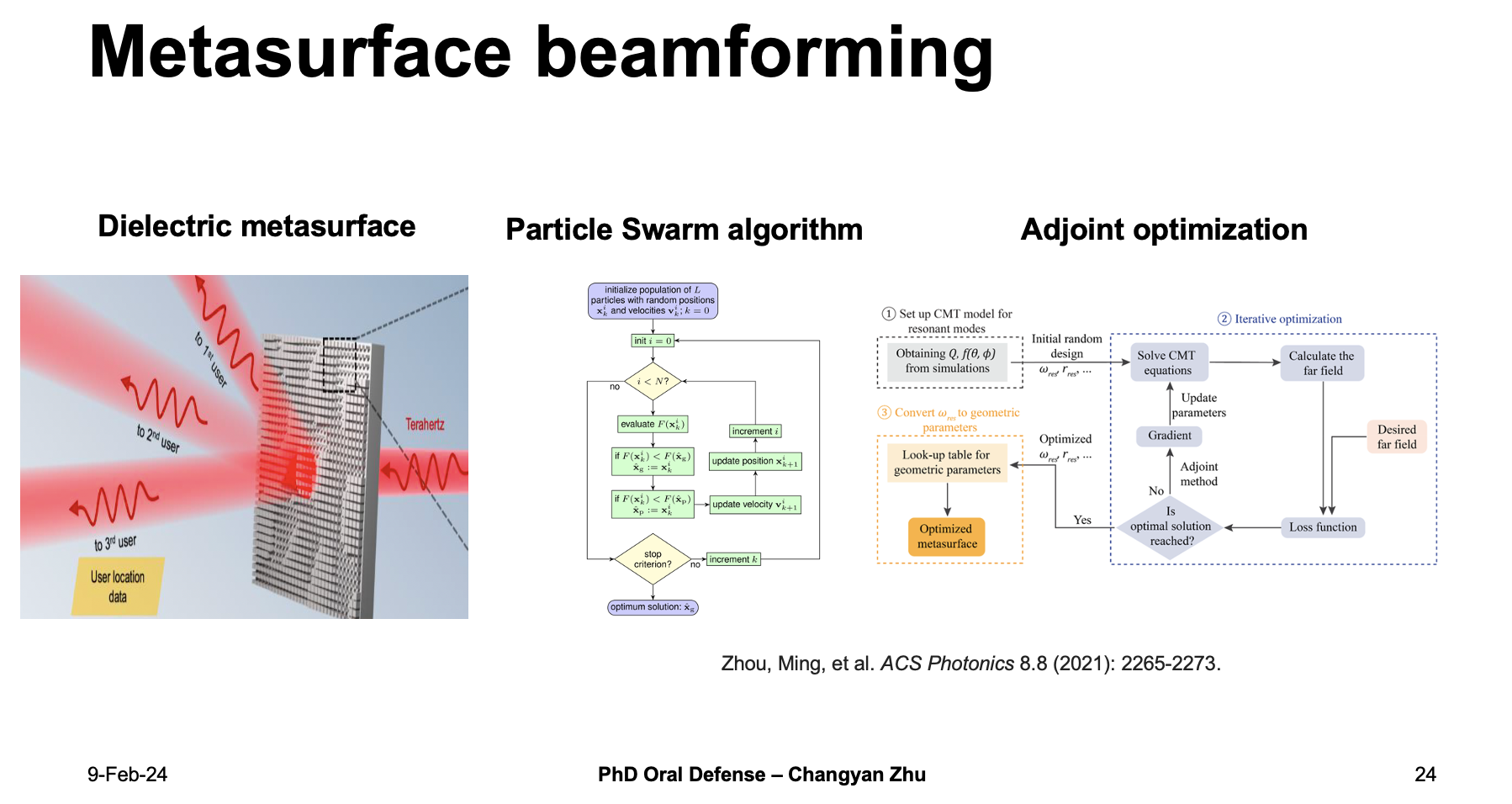
To achieve this, we can use a dielectric metasurface and tune the phase profile dynamically. Doing so requires an optimization algorithm either by particl swarm algorithm or adjoint optimization methods. However, both methods require iteratively updating the parameters that cost of a larage amount of time, which may increase the data response time. To overcome this, we decide to use a machine learning scheme because machine learning usually requires much less time to do a forward passing.
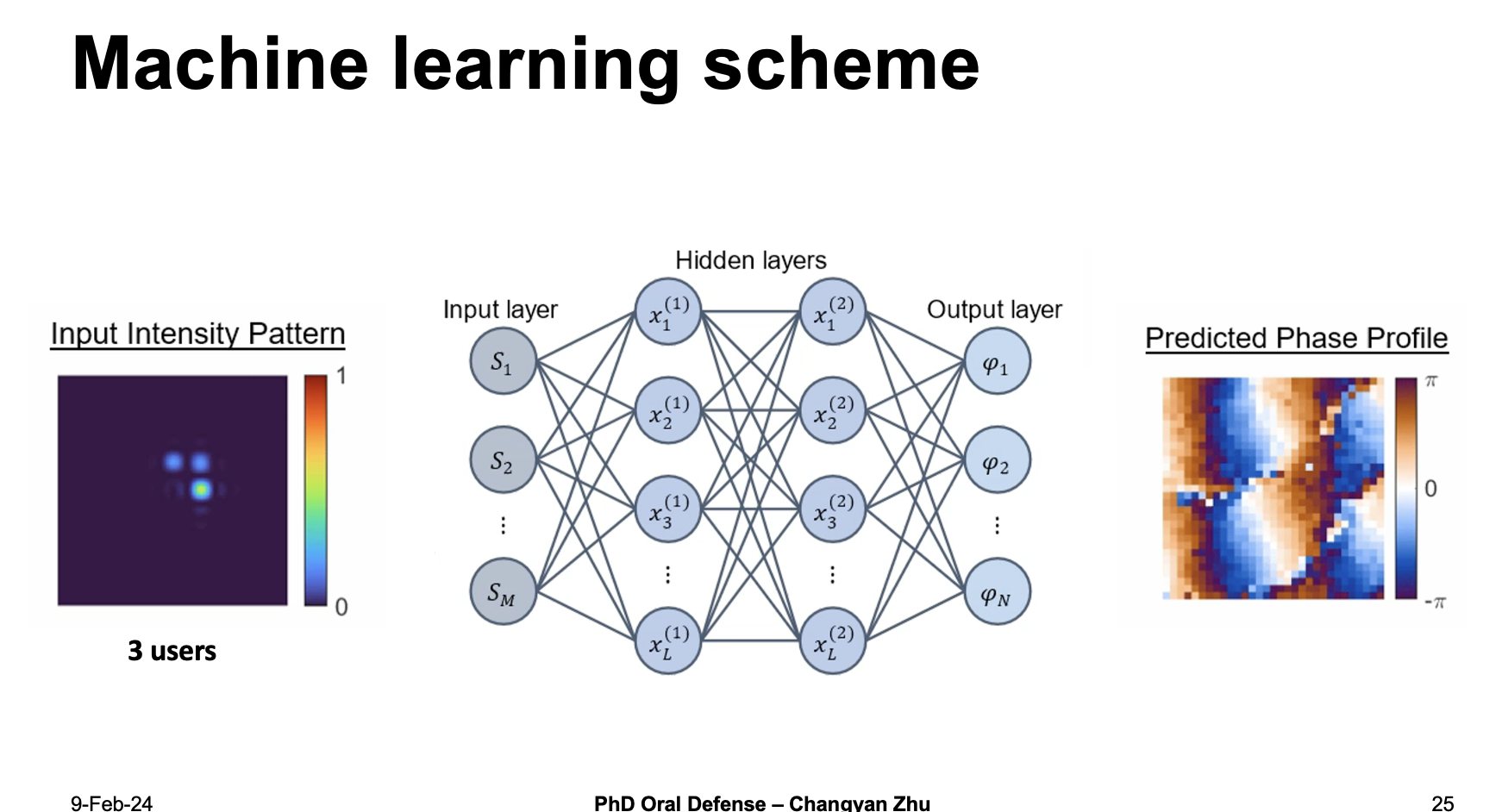
The machine learning scheme we choose consist of a two hidden layer dense neural network with input intensity pattern and predicted phase profiles.
For demonstration purpose, we use a dataset consist of up to three users. After training, we use it to predict phase profiles and generate the predicted intensity pattern to compare to the input intensity patterns.
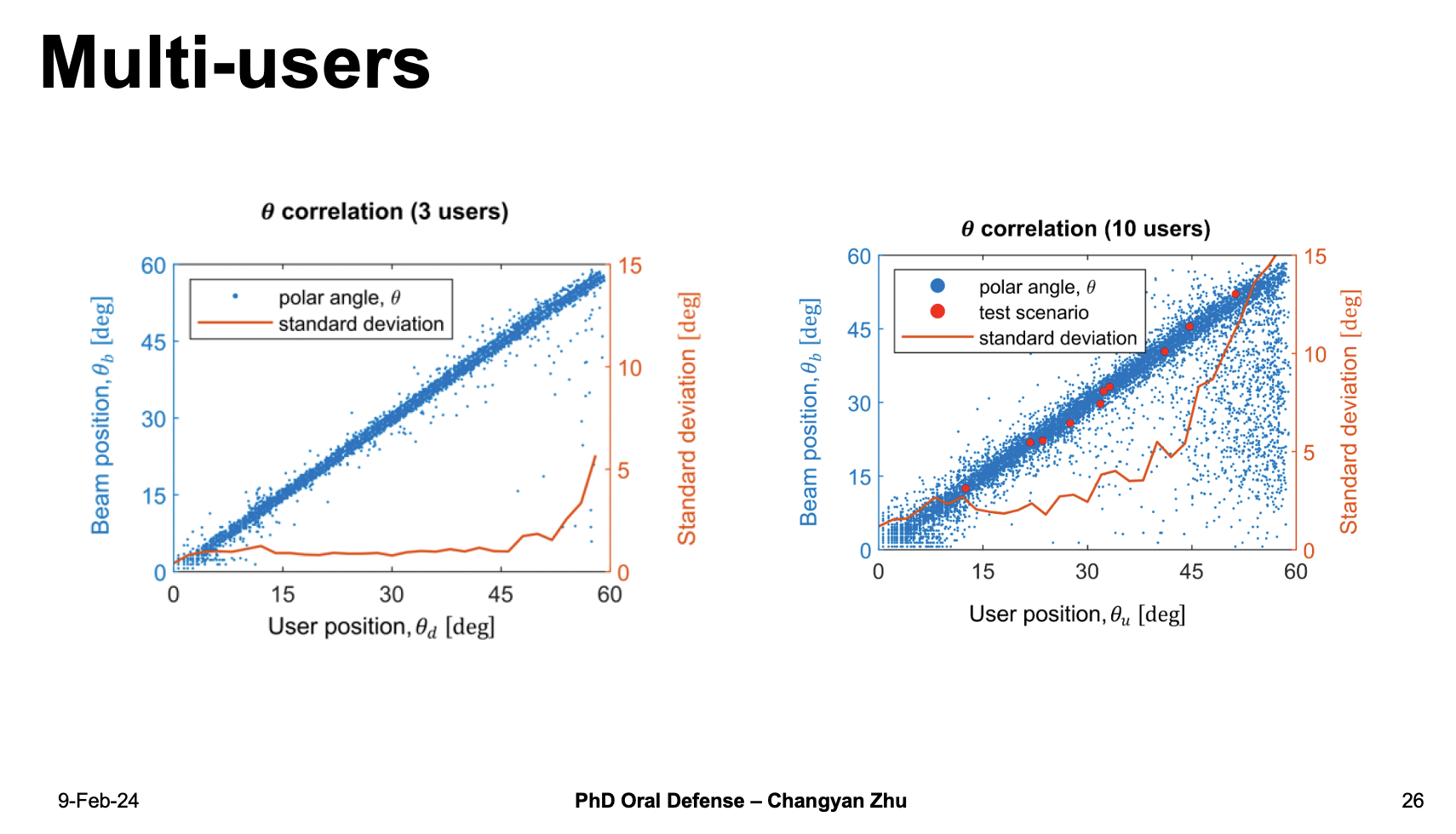
For 3 user case, most of the beam positions matches very well with the user positions. And what suprisingly is even with 10 user reconstruction the machine learning scheme can still give very accurate predictions with a standard deviation lower than 15.
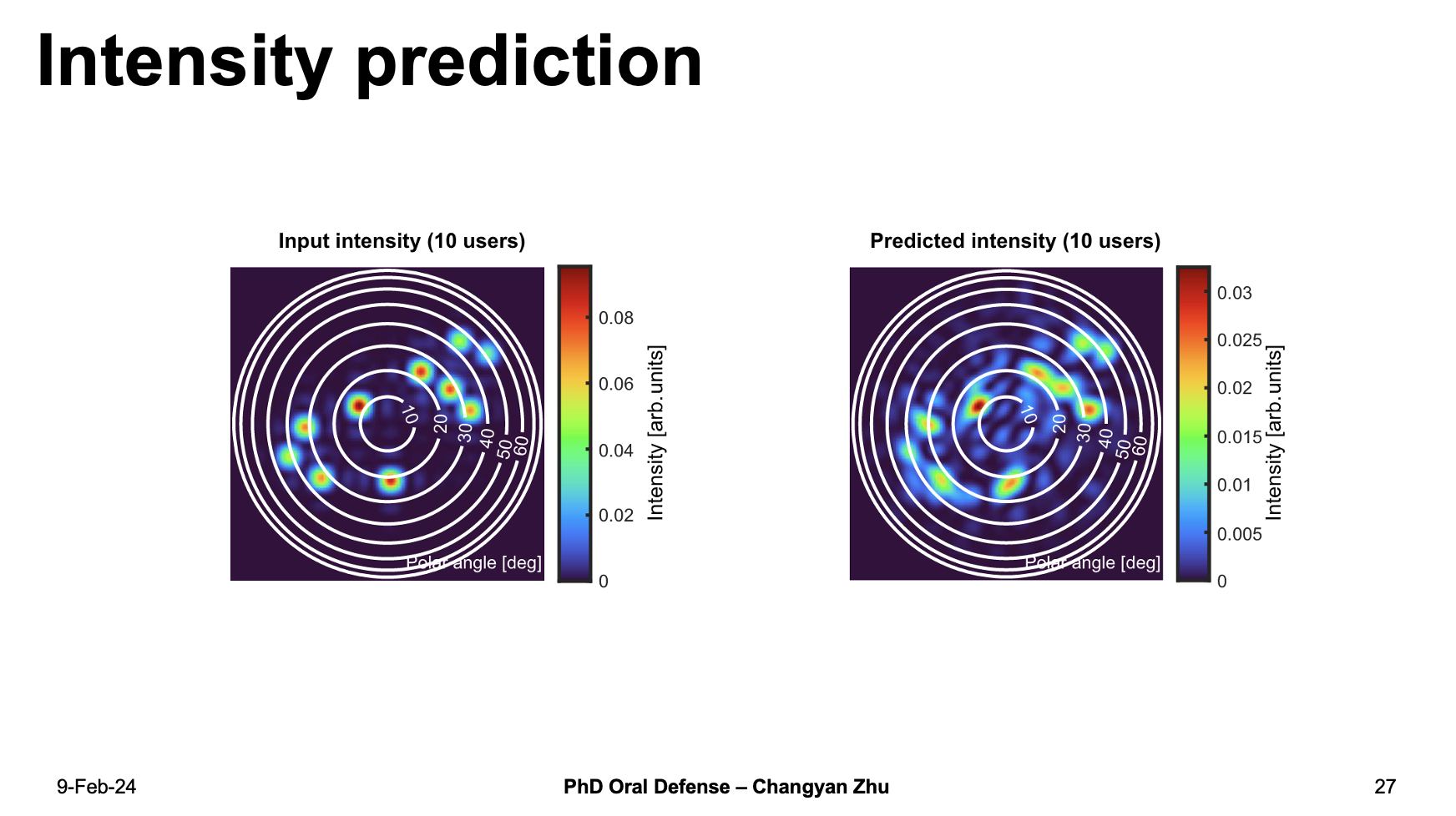
The intensity patterns show here also indicate that the machine learning predicted beam positions matches very well even up to 10 users.
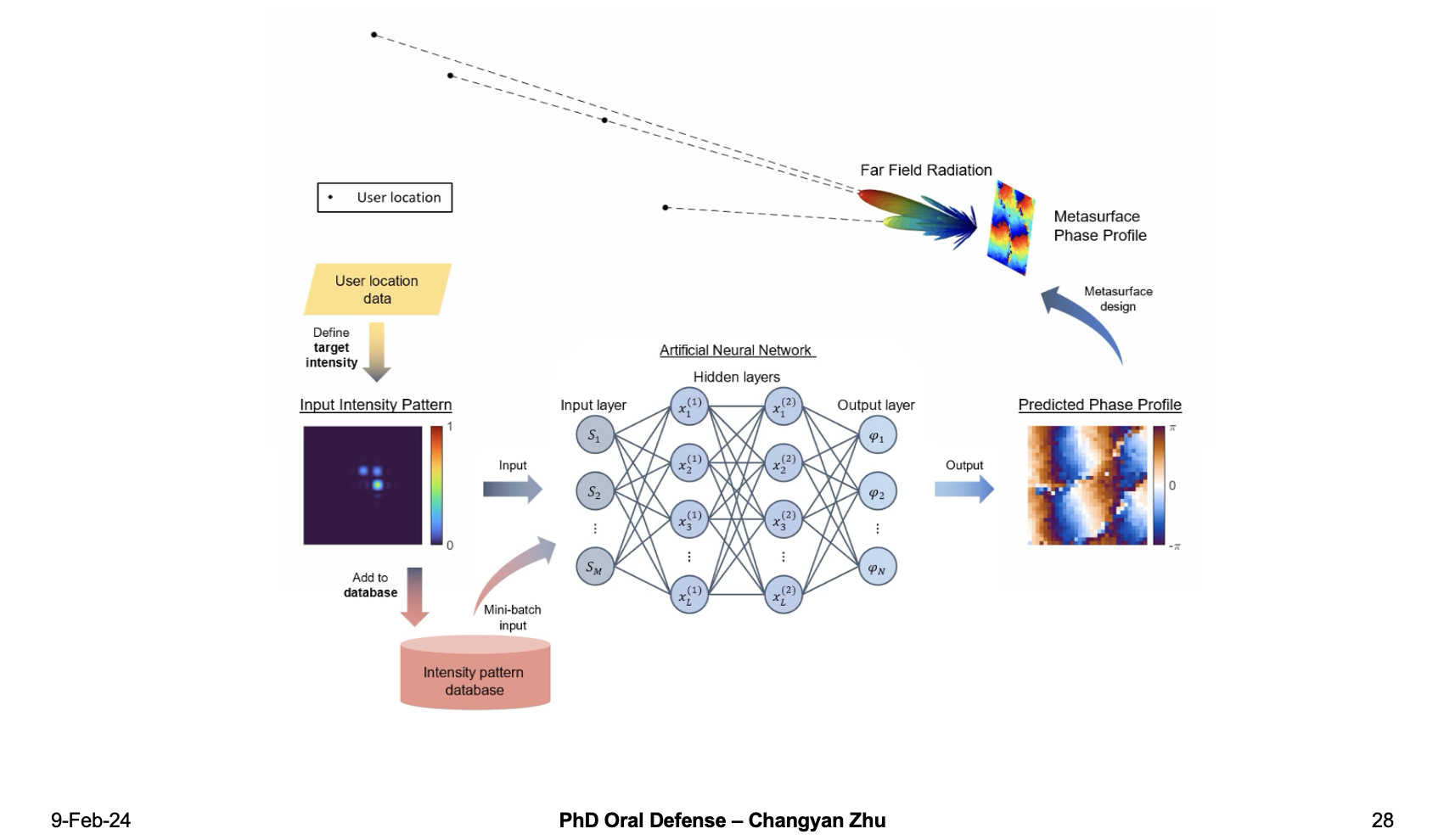
Based on the machine learning model, we can now introduce a self-adaptive real time terahertz beam forming scheme which use machine learning to predict the phase profiles, and combine it with user location data, they are send to an ever-growth database which can be used to further imporve the neural network accuracy.
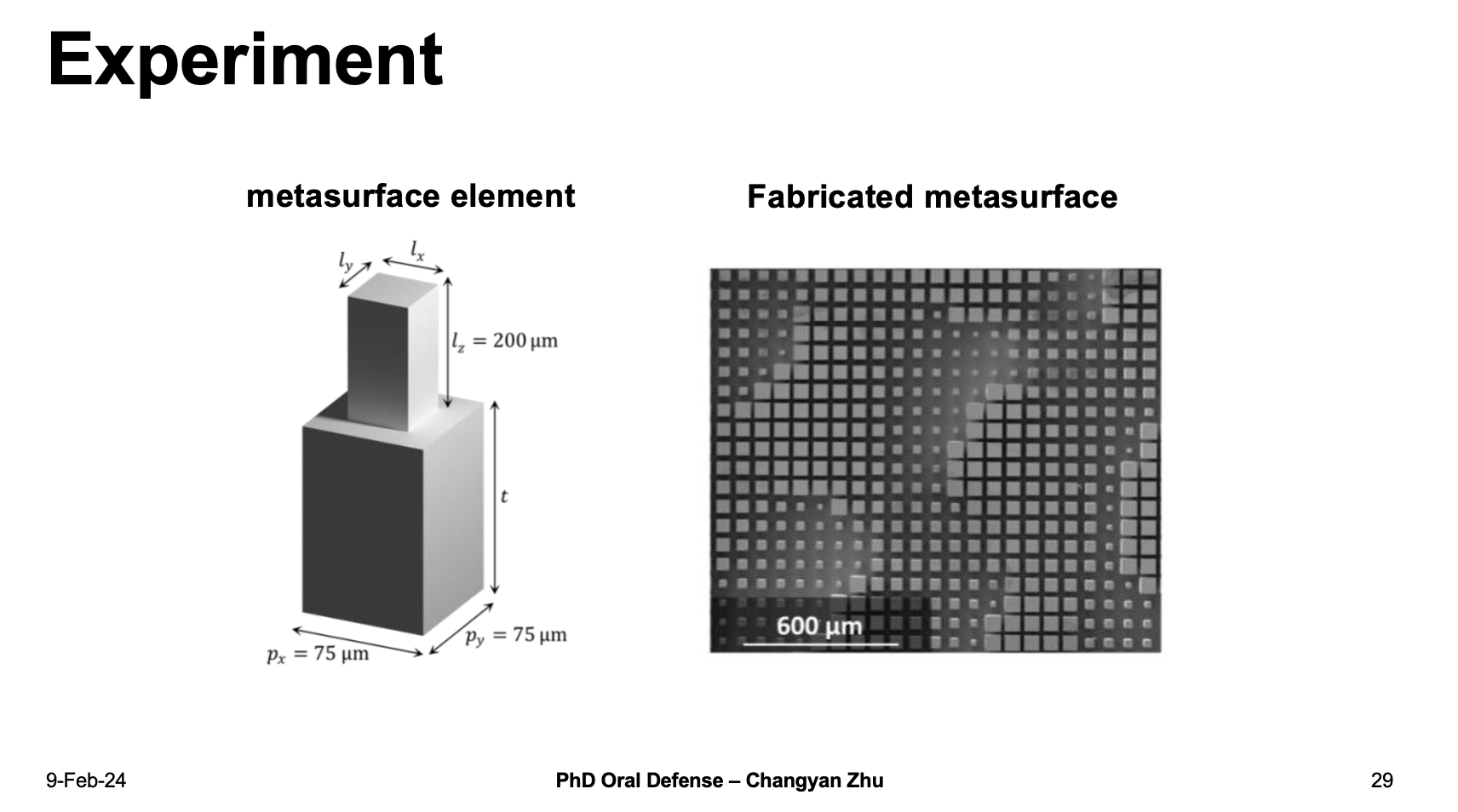
To demonstrate this in experiment, we use a machine learning predicted phase profile to fabricate the metasurface,
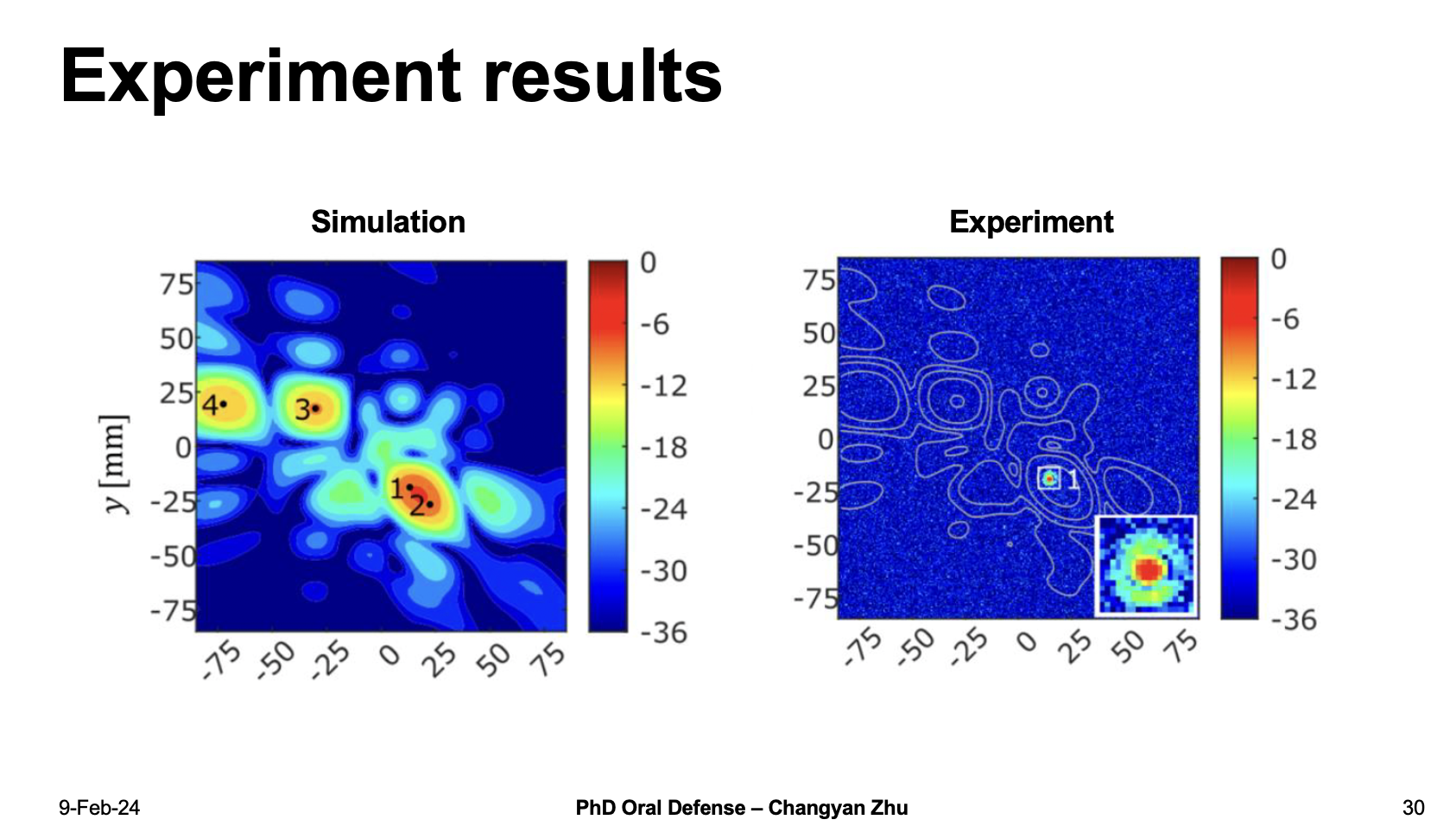
The experiment results show that experimental measured peaks match very well with the simulation peaks. It is important to note that there is only one peak shown in experiment figure because our THz detector has a small angle range, therefore we can only detect one peak at a time, I have also include other peak positions in my thesis.
4. random spectrometry
Now we have shown that machine learning is able to achieve MMF image reconstruction as well as terahertz beam forming. In photonics, the analysis of optical components are also very important. To accurately analyze the optical spectrum, a spectrometer is needed.

Talk about spectrometer, we will immediately think about the Prism, which Issac Newton had used to analyse the sun light spectrum. Basically it is because different wavelength of light progating with a different phase velocity in the glass. Similar to this, a diffactive grating design can also be used for spectrometer. In both systems, the resolution of the spectrometer is related to linear dimension of the systems.
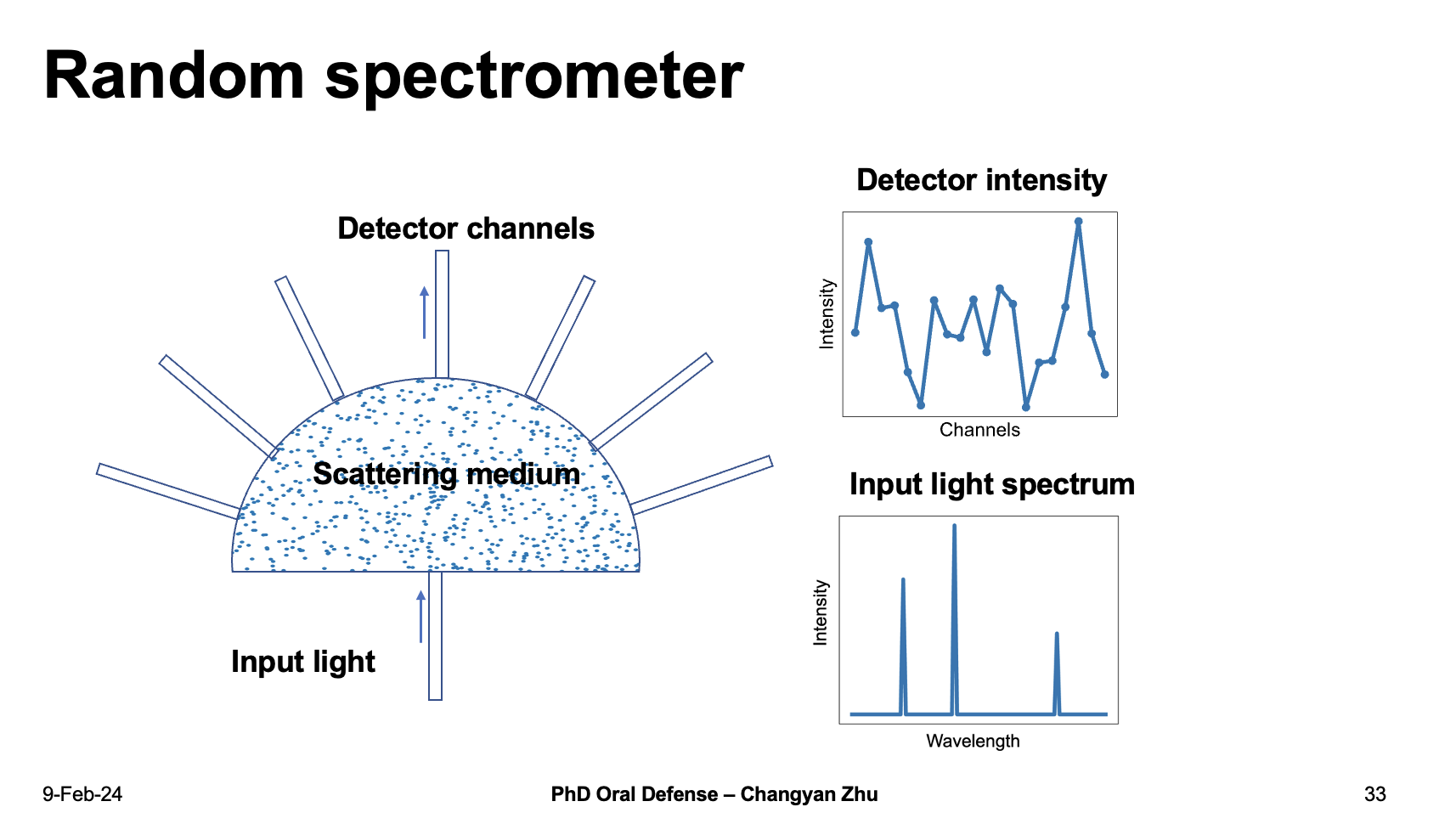
To further improve the resolution with a small footprint, people have come up with a smart way by using a random scattering media to fold the optical path of light, which becomes a random spectrometer. Random spectrometers enable optical paths larger than the linear dimension, however, the detector intensity need to be further reconstructed to know the input light spectrum.
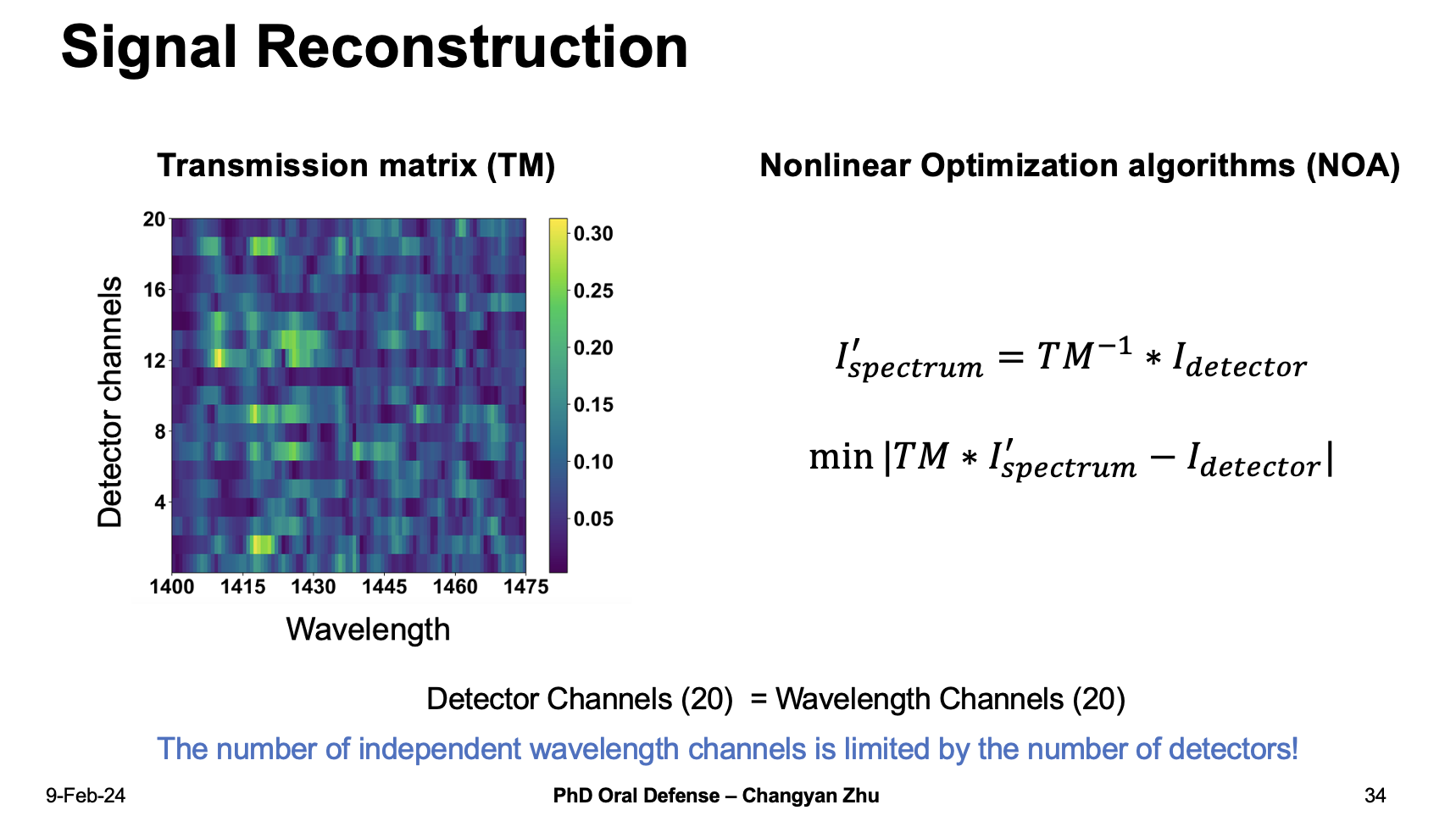
A conventional way to do this is to calibrate a Transmission matrix. If we take a single peak spetrum into the spectrometer, we will get a distribution of detector channel intensities, by doing this for the whole working bandwith, we obtain a transmission matrix or TM.
Then we can calculate the spectrum by multiply the inverse of TM to the detector intensities, to further reduce the error, we can use nonlinear optimization algorithms (NOA).
However, by using the transmission matrix inverse we need to ensure that the detector channels are equal to wavelength channels, then the number of independent wavelength channels is limited by the number of detectors!
Will machine learning bring new hope this time?
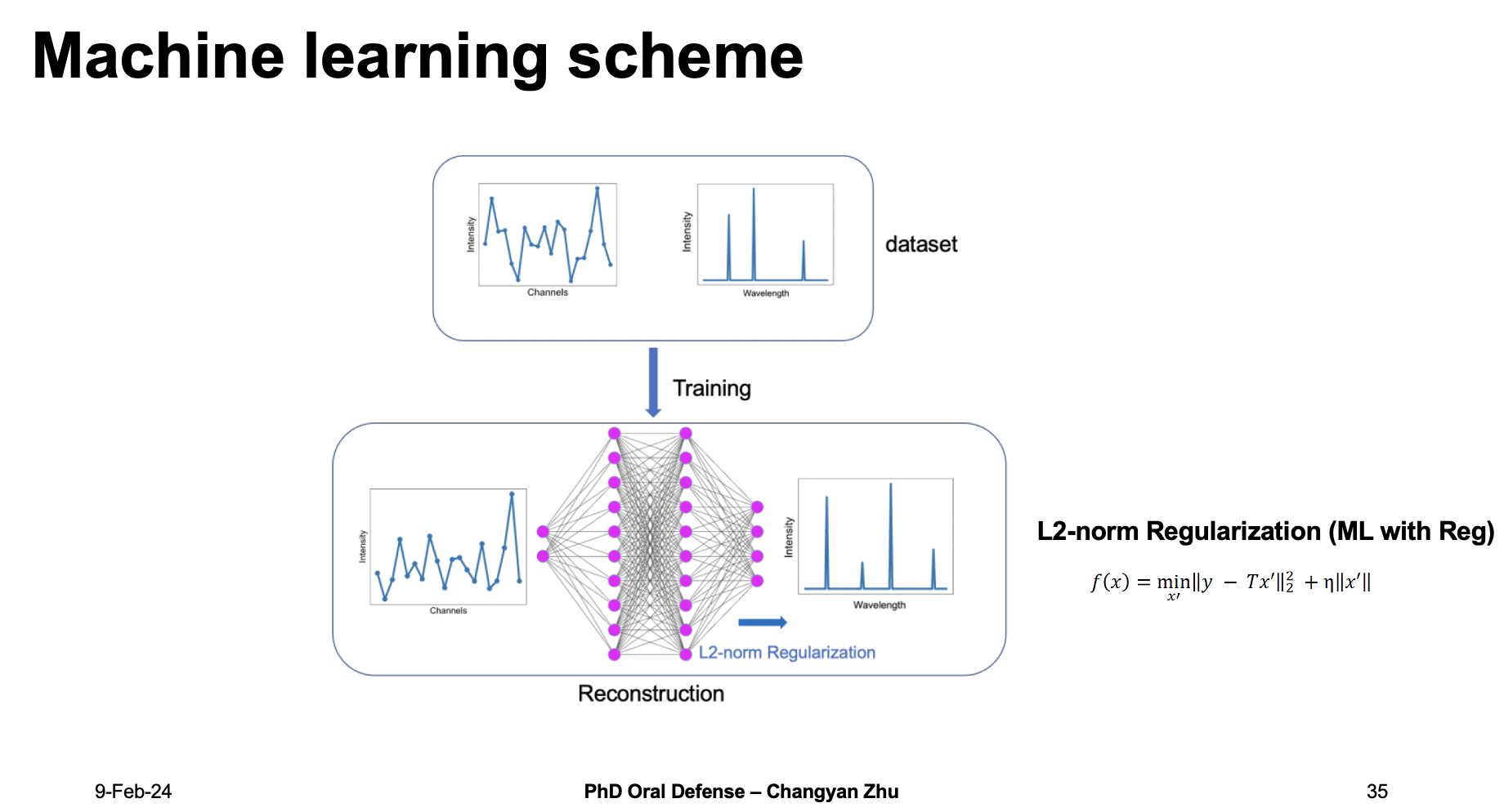
The answer is stil yes. Because machine learning doesn’t require the input and output dimension to be the same. Therefore, we can generate dataset and feed into a neural network again. This time, to reduce the error, I chose to use a L2-norm regularization (ML with Reg). I will show the neccessity of addiing regularization later.
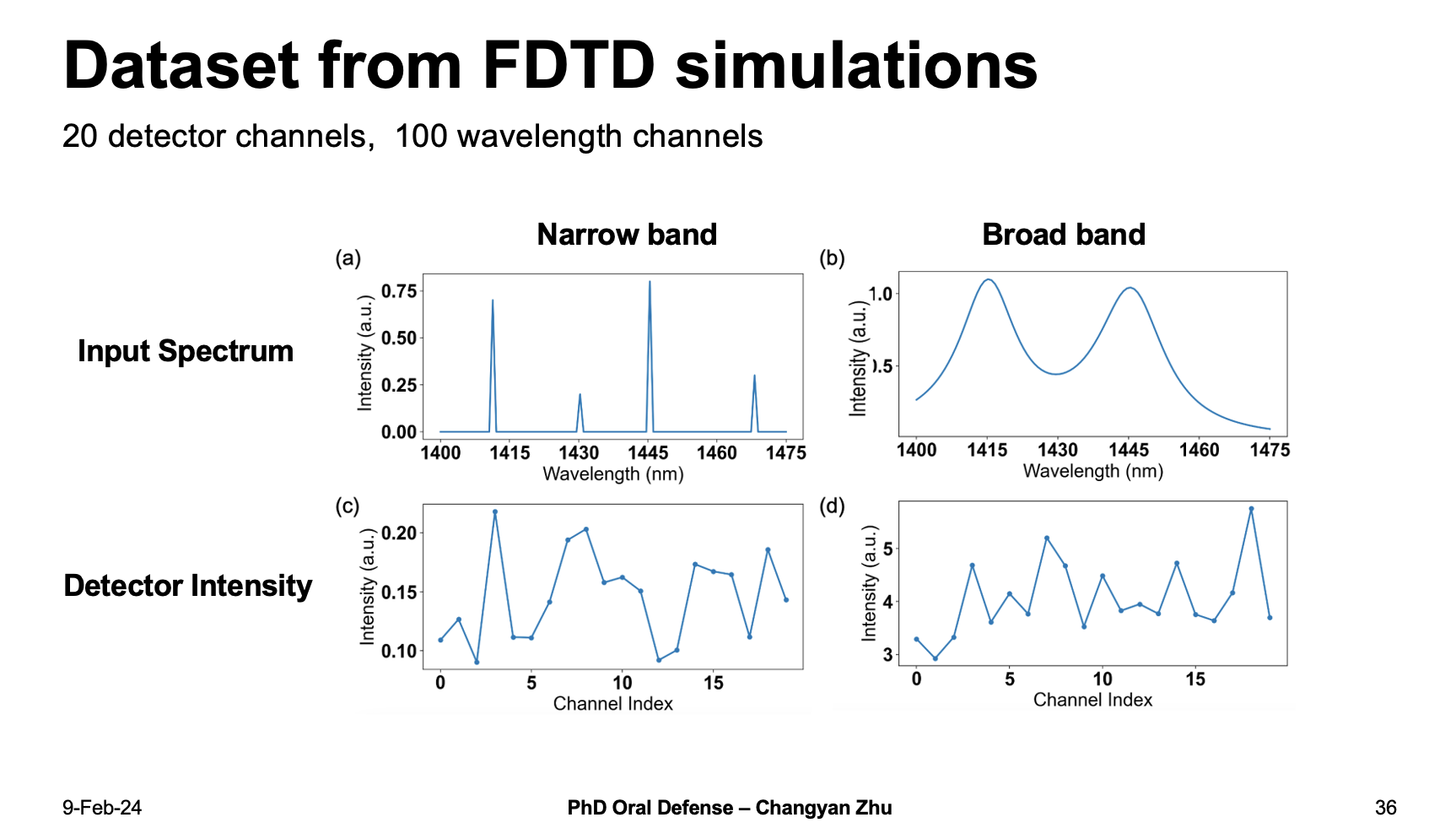
We are using a dataset generated from FDTD simulations, as for the input spectrum, we chose a combination of both narrow band and broad band signals. The narrow band signals consist of several peaks and the broad band signals are continuus wavelength channels.
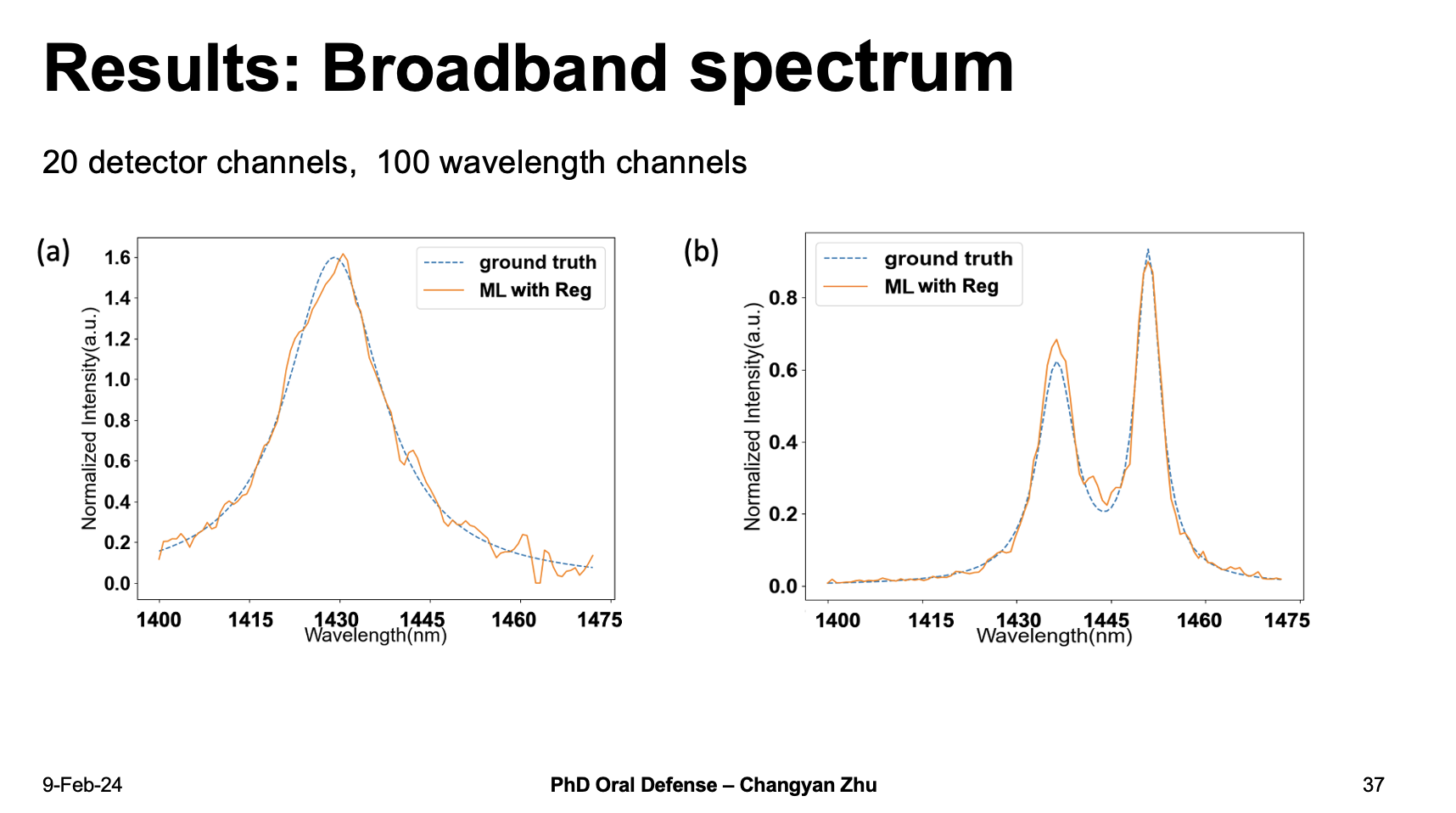
Let’s take a look at the broadband spectrum first. The machine learning actually give very good predictions even with 100 wavelength channels which are much larger than 20.
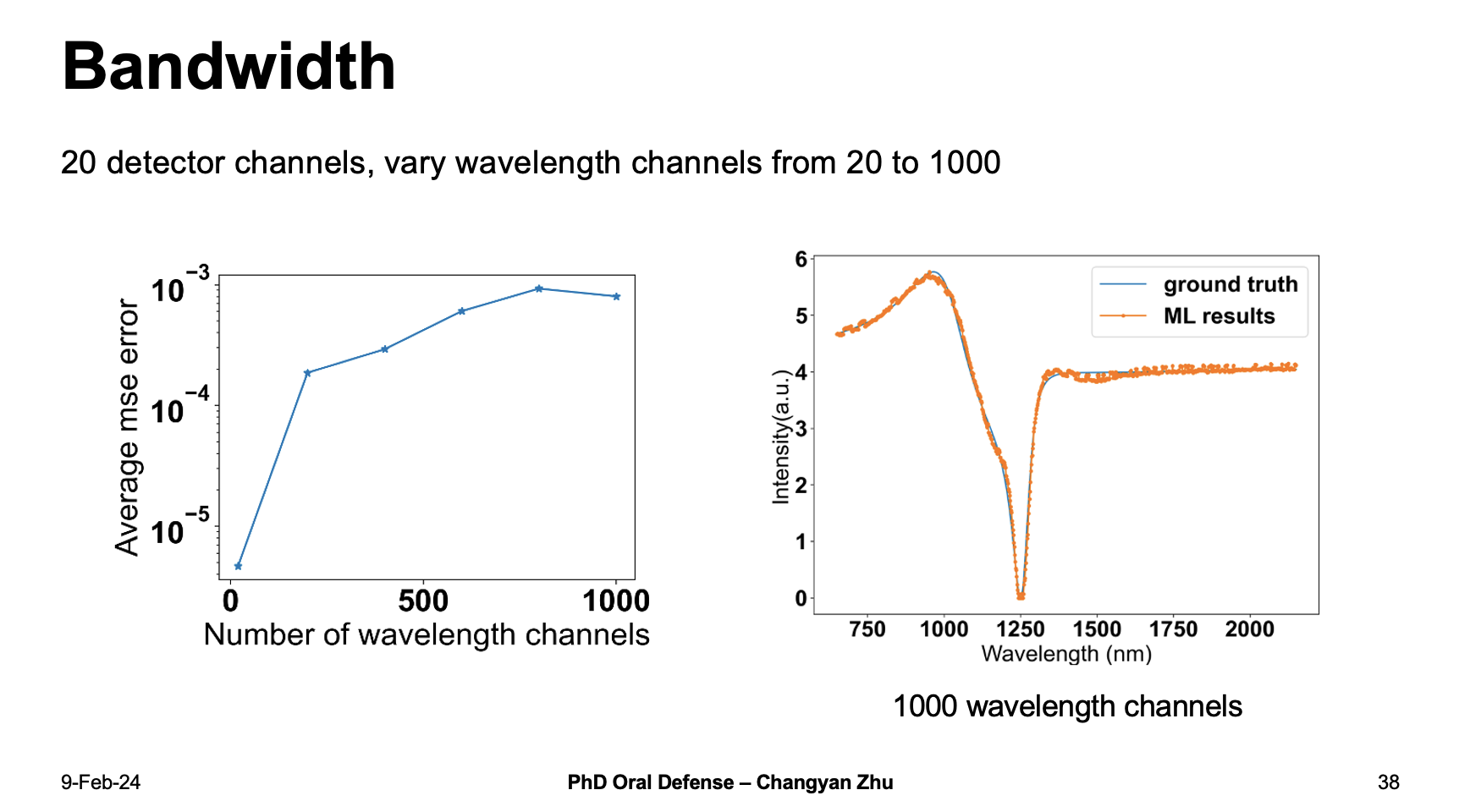
In order to know the limit of bandwidth that machine learning can achieve, we further increase the wavelength channels up to 1000, even the average MSE error goes higher, the reconstructed results for 1000 wavelength channels still give very accurate predictions. We noticed that the experiment error make a much larger impact on the signals at the stage, so there is no need to further increase the wavelenght channels.
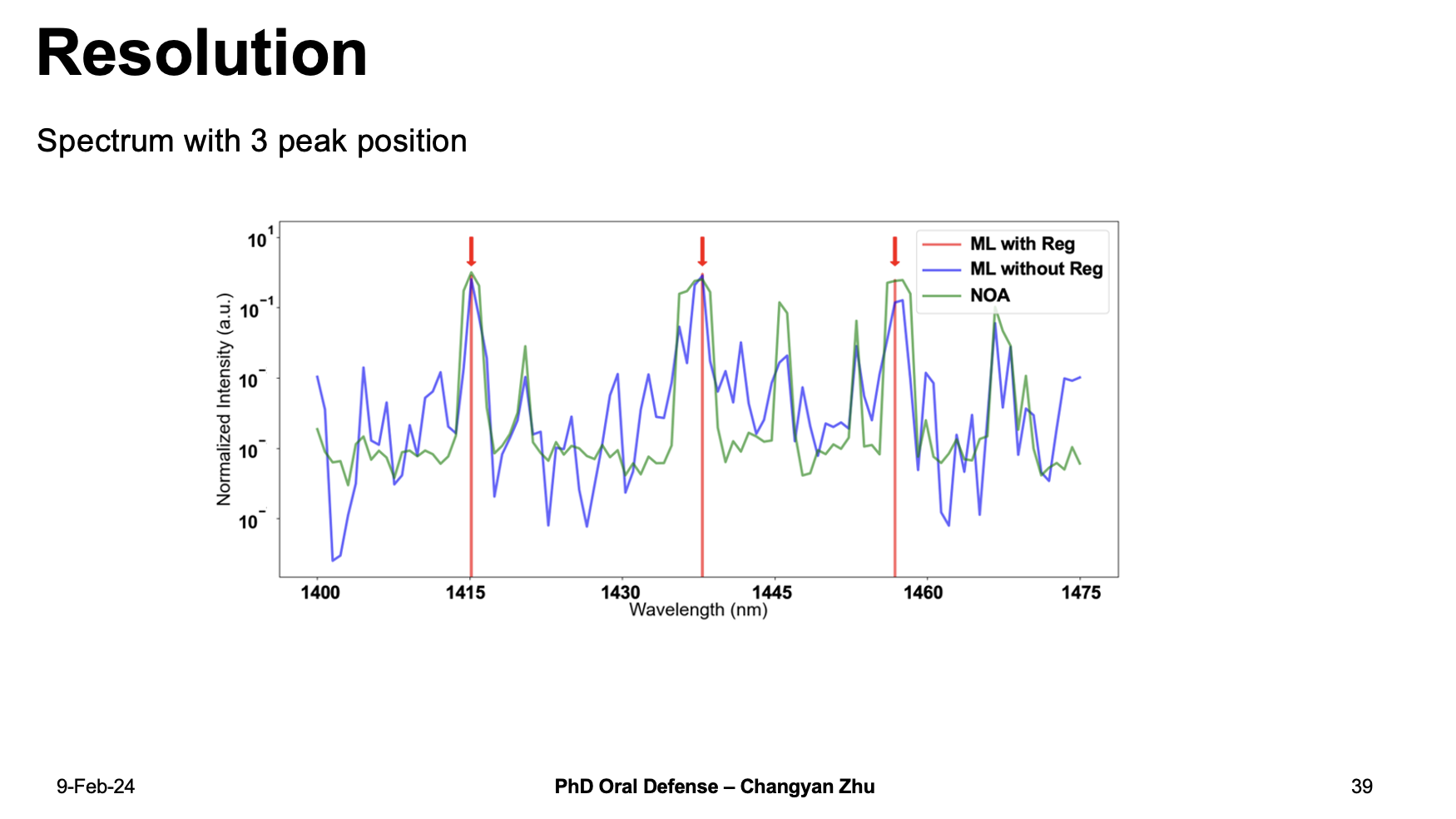
Besides from bandwidth, the resolution is also a very import metric for random spectrometers. In this figure, we show the reconstructed results for a 3 peak input spectrum. The positions of the 3 peaks are labeled by red arrows, compared to NOA or ML without Reg, the ML with Reg gives nearly perfect reconstruction results for the peak positon.
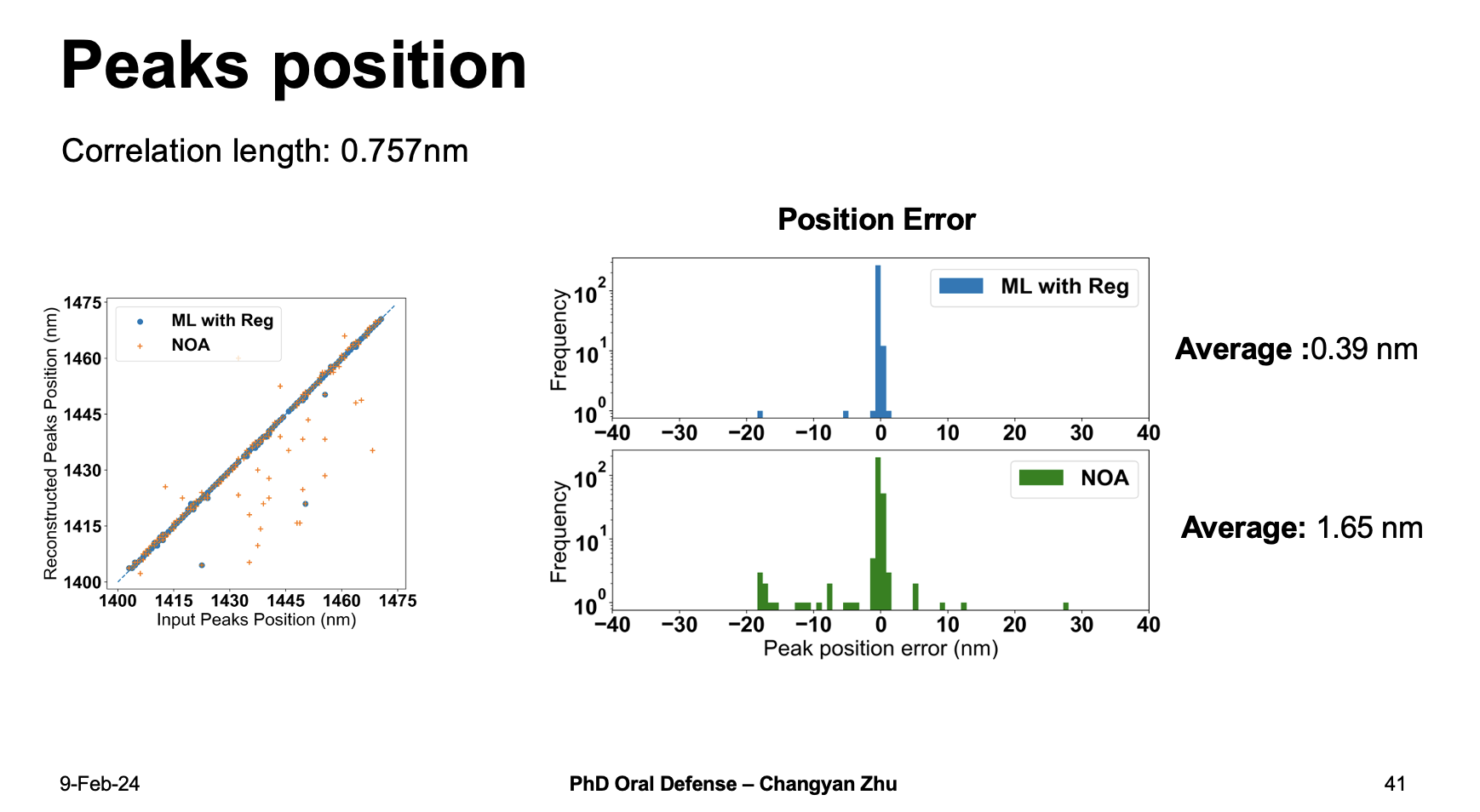
If we compare the reconstructed peak position and input peak position with 200 samples, we can see that most of ML with Reg results are located at center, which means the error is small. By calculating the average position error, the ML with Reg shows an average value around 0.39 nm which is much better than 1.65 nm for NOA methods.
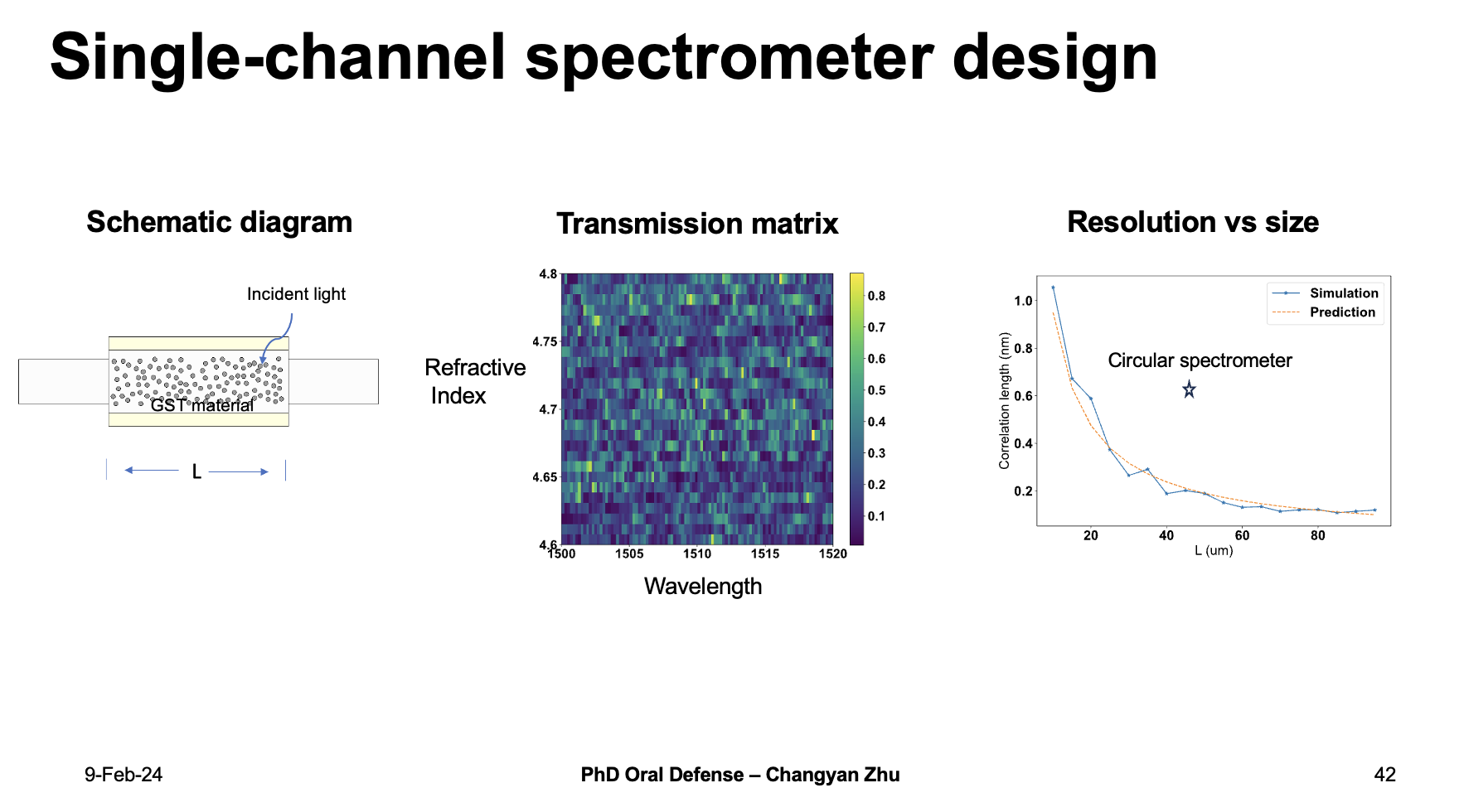
In order to further reduce the footprint of random spectrometers, I propose a single-channel spectrometer design here. We have introduced the transmission matrix for spectrometer previously, the wavelength define the rows and the detecotr channels define the columns. However, for comlumns they don’t have to detector channels, but any parameters that can be tuned repeatedly, for example, the refractive index.
GST material is known to experience phase transtion with incident light so it could be used as a ideal platform to achieve this. I also done fdtd simulations and vary the length of the single-channel spectrometer design, the results show that the single channel design can achieve better resolution with a smaller footprint compared to cicular spectrometers.
5. non-Hermitian physics
Most of the above projects have been focused on using supervised learning in a more engineering way, there are also other types of machine learning methods, for example unsupervised learning which are generally used for dimension recuction and clustering.
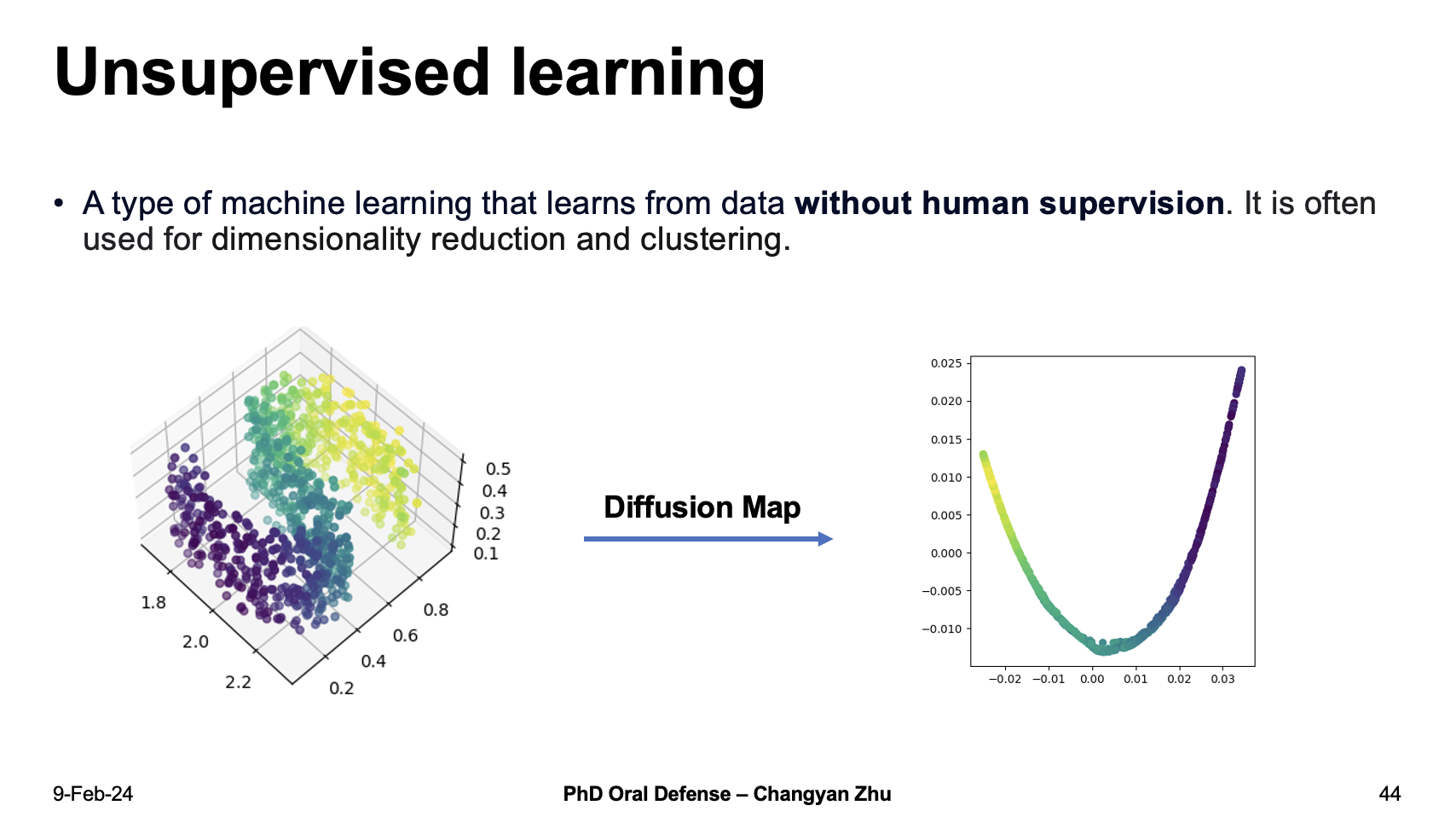
A tyipcal algorithm is called difussion map. For example, the letter “S” in the three dimensional space can be reduced to a two dimensional representation by using diffusion maps.
With diffusion map, we can do many other things.
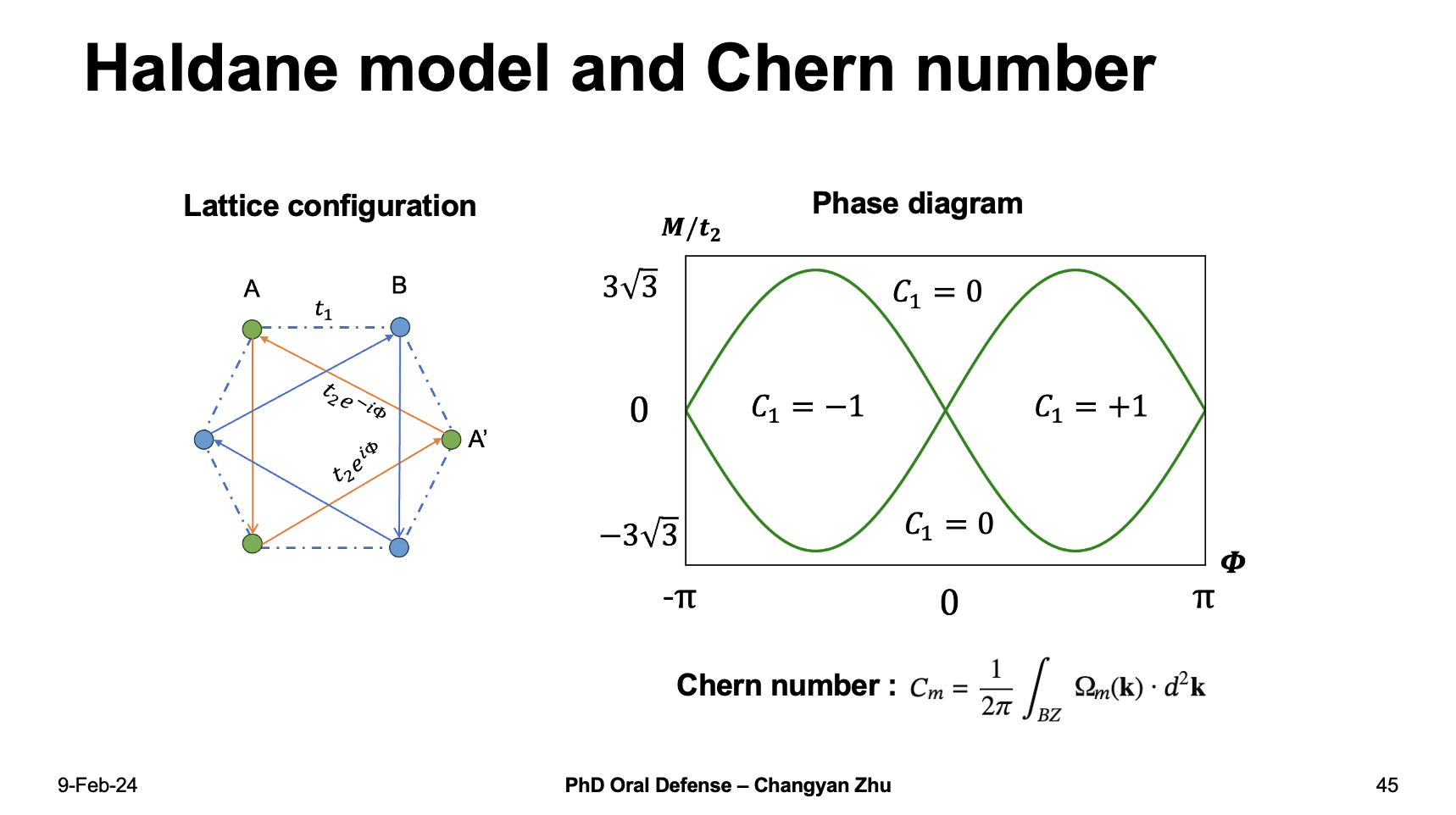
For example, the haldane model is well known for its next-nearest neighbor hopping phase, by tuning which we can obtain a phase diagram which include different chern number.
Can diffusion map used to identify chern number?
One would argue why wouldn’t just calculate the chern number based on the k-space hamiltionian?
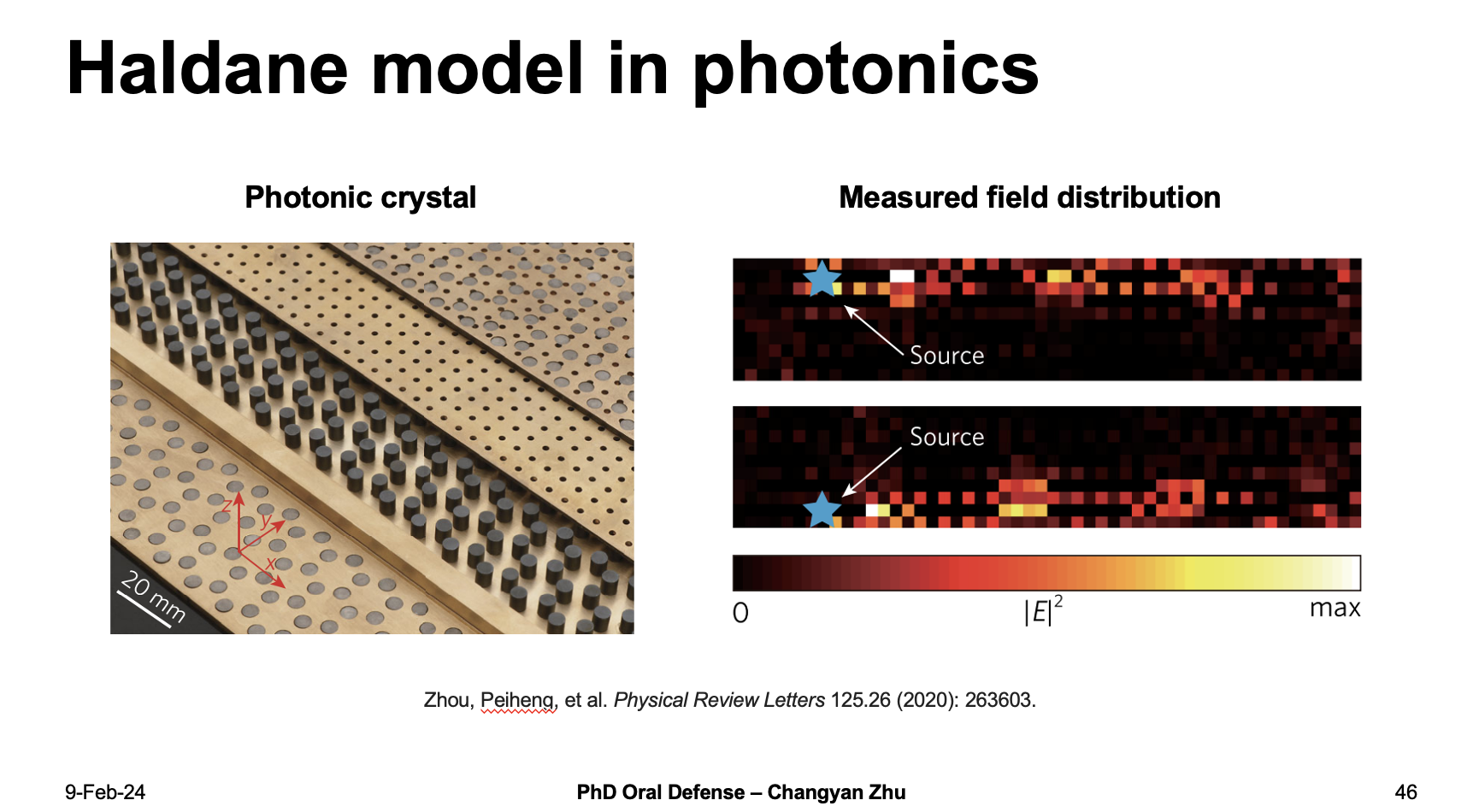
However, sometimes it may not be easy to achieve, For example in a photonic crystal version of haldane model, you can only measure the filed distribution which are basically eigenvectors, can we use those eigenvectors to identify chern numbers?
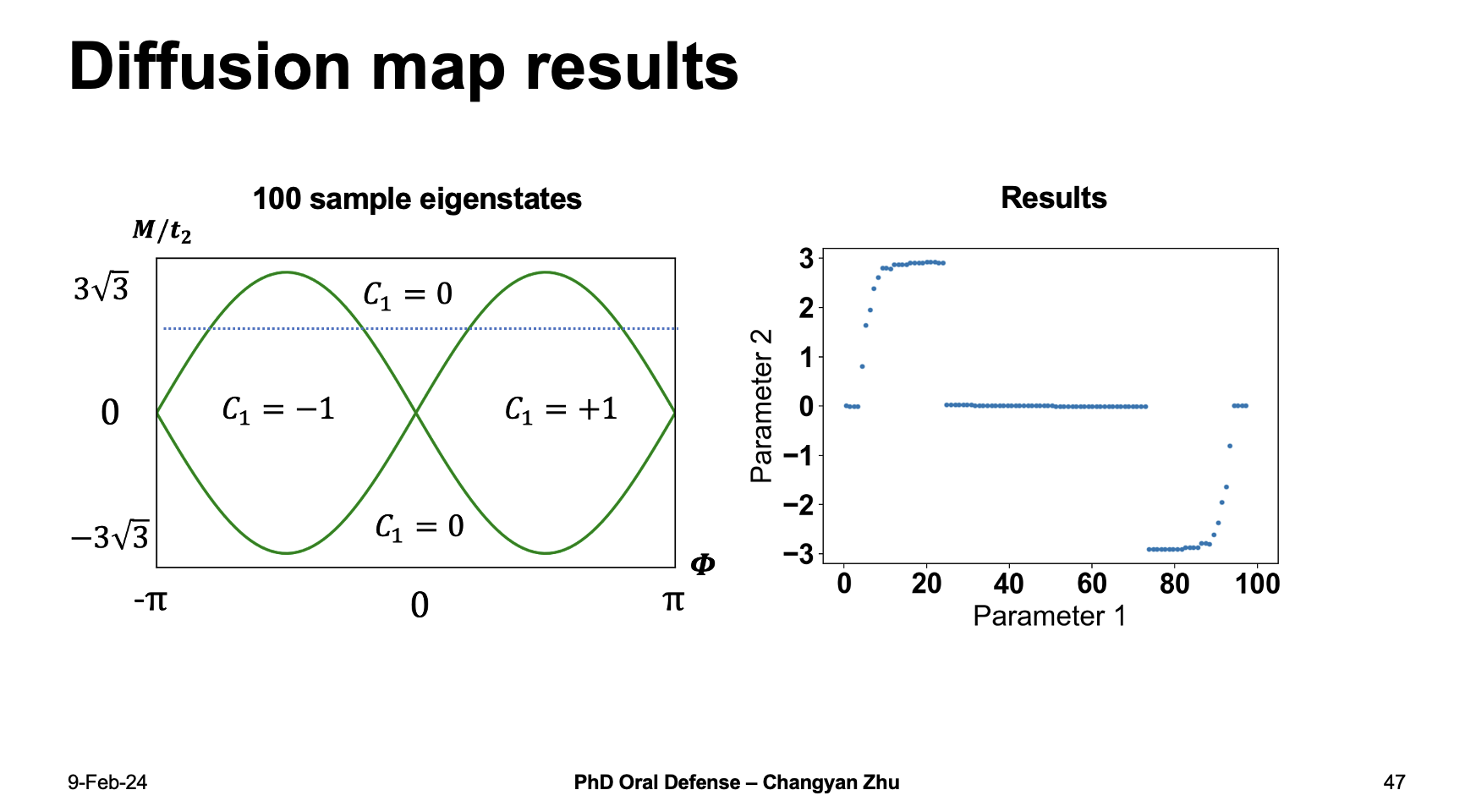
We design a dataset which includes 100 sample eigenstates by varying $\Phi$ from $-\pi$ to $\pi$, therefore there are five different stages for the dataset. When we feed the dataset into difussion map algorithm and reduce it into 2 dimensional space, the results successfully represent five different stages, Therefore, unsupervised learning methods can be used to identify topological invariants.
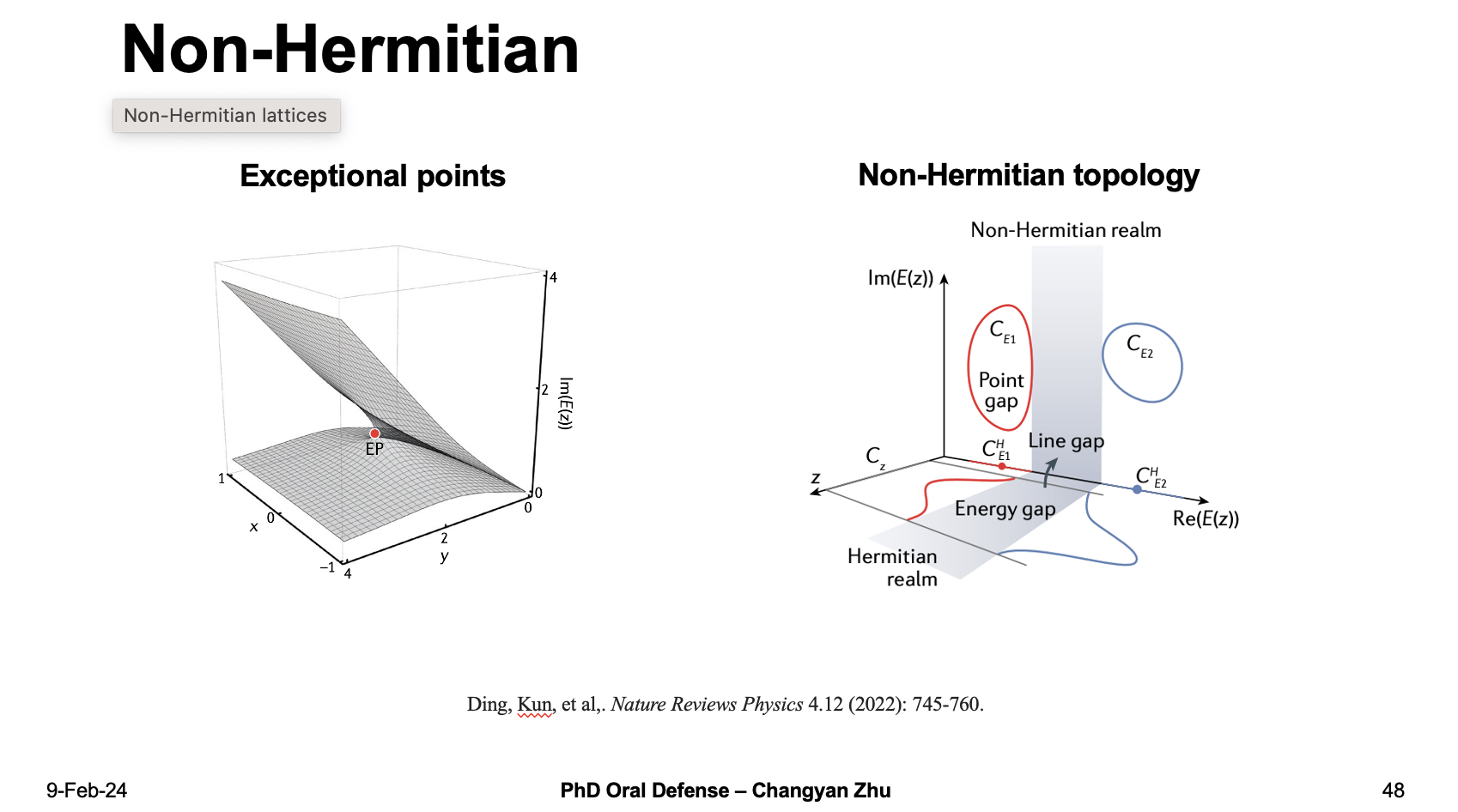
Compared to Hermitian systems, in non-Hermitian systems there are no guarantee of real eigenvalues or orthorganol eigenstates, therefore exist many new phenomena such as exceptional points or non-Hermitian topology.
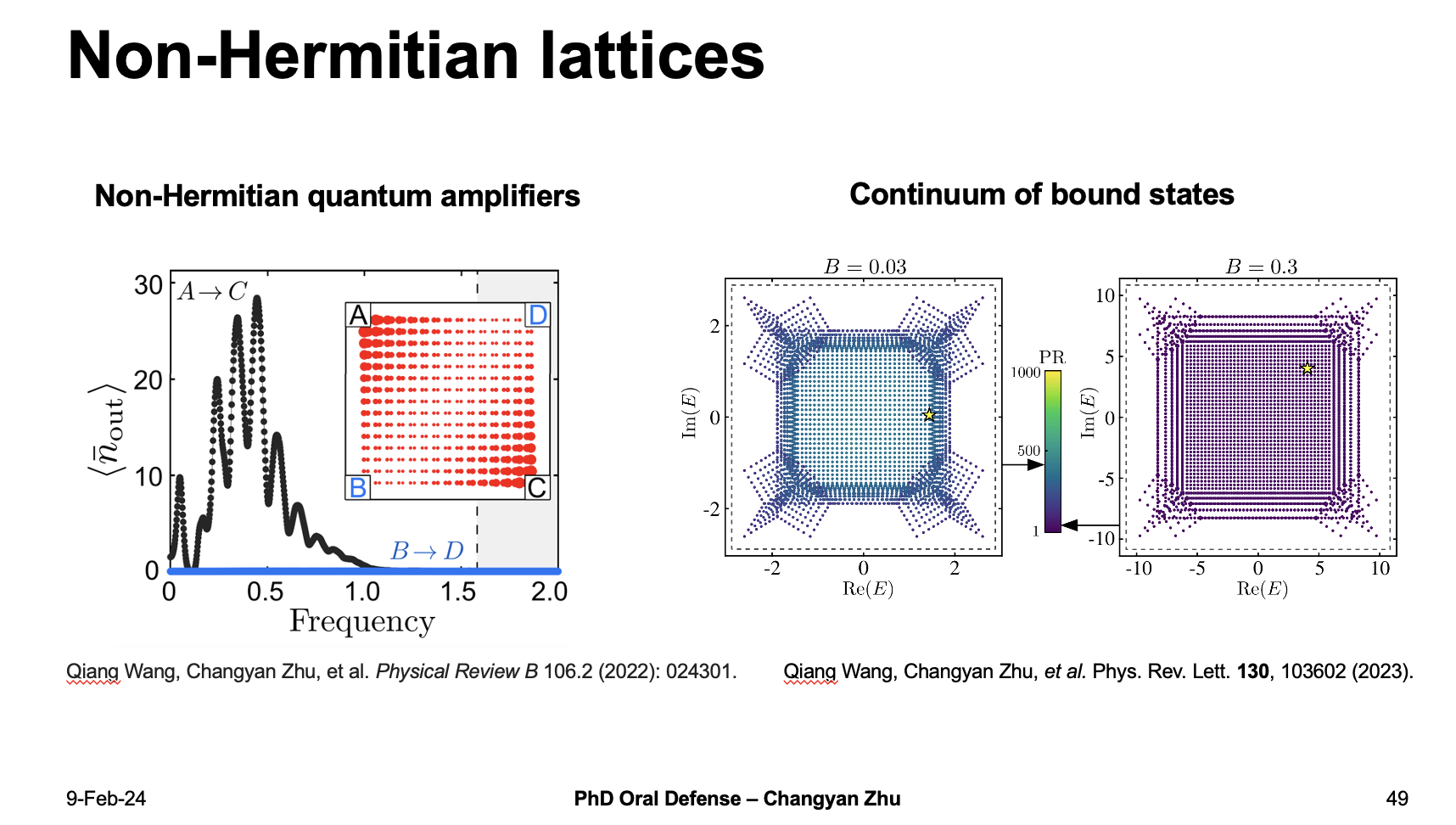
I have also done investigation on non-Hermitian systems and found two kind of non-Hermitian hamiltonians including non-Hermitian quantum amplifiers and continuum of bound states in complex energy plane.
Can we use machine learning methods to identify the boundary between Hermitian and non-Hermitian systems?
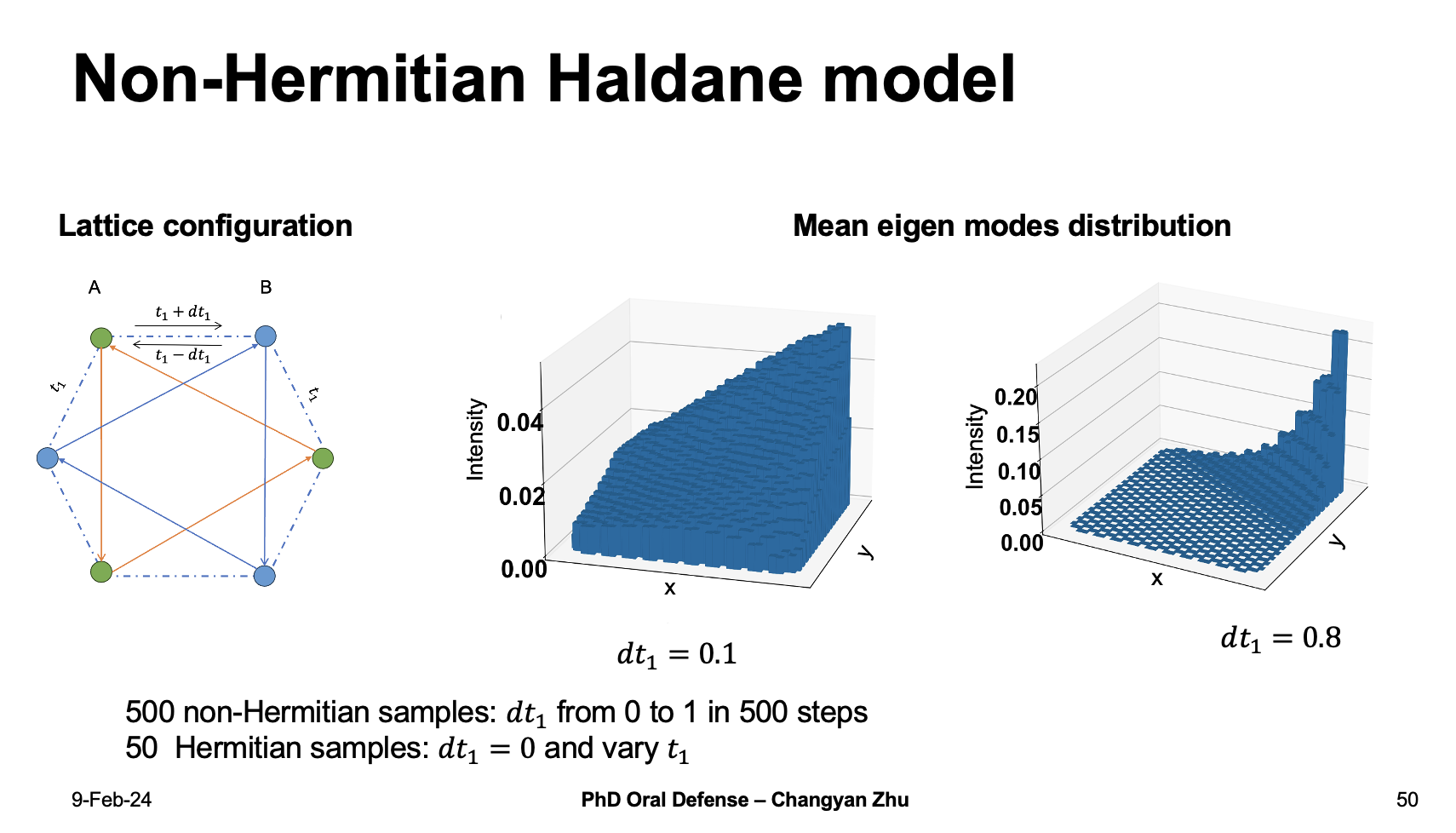
Here we design a test based on a non-Hermitian haldane model which use non-reciprocal coupling by adding $dt_1$ on $t_1$. We collected 500 non-Hermitan samples where $dt_1$ vary from 0 to 1 and 50 Hermtian samples where $dt_1 = 0 $ and $t_1$ at different directions are varies.
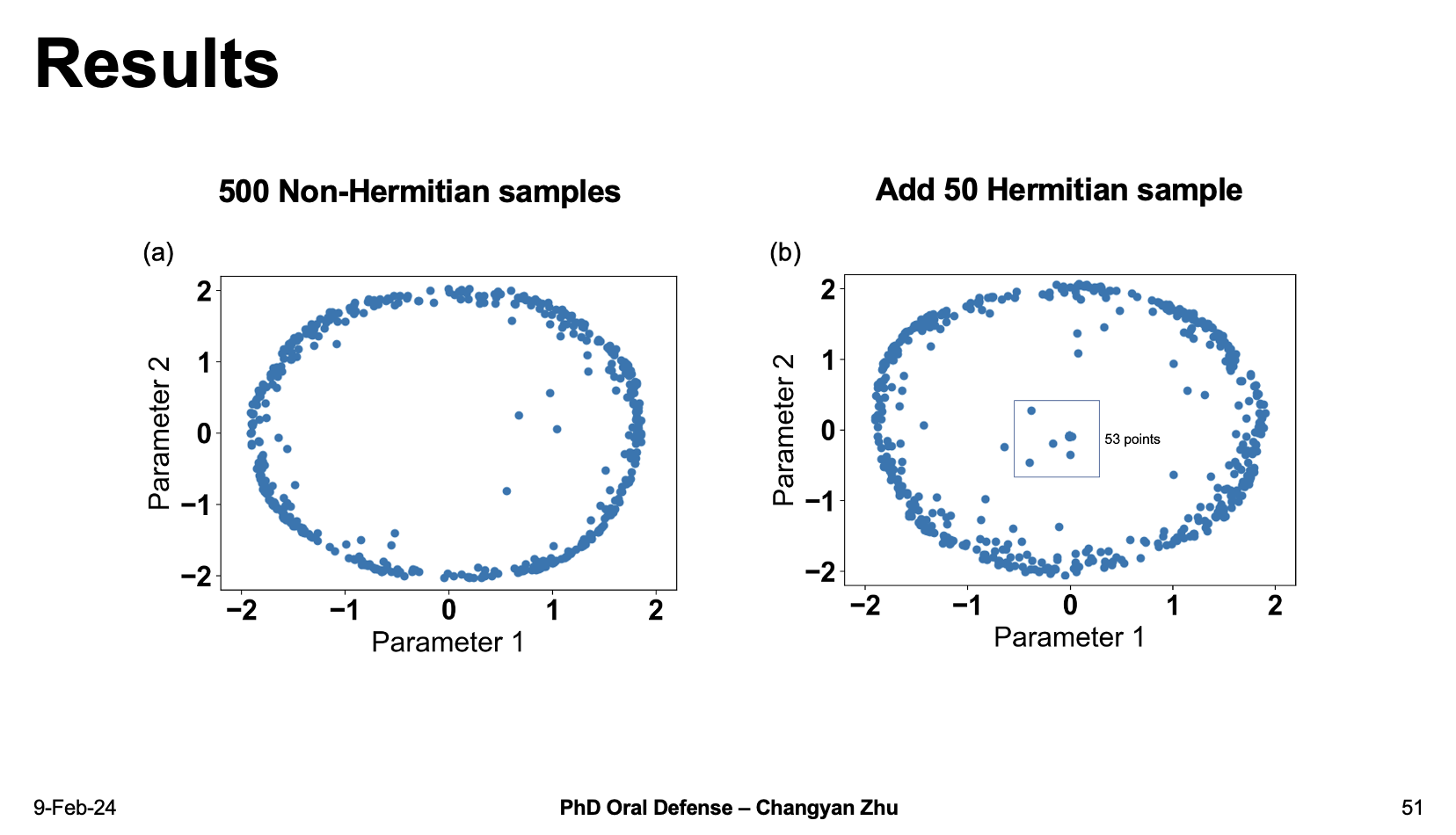
The difussion map return a circular shape for 500 samples, while we add 50 Hermitian cases in to the dataset, all of them are located at the center of figure. That shows an obvious distinction between Hermitian and non-Hermitian systems, therefore we have shown that unsupervised learning methods can be used to identify them.
6. Conclusion and future work
Given the discussions above, we now come to the conlusion part.

In conlusion, we have demonstrate the ability of machine learning methods in transmission of images in MMF with intensity-only detection. Particularly, SHL-DNN outperforms U-net in terms of training time and fidelity.
Real time terahertz beam forming and High-accuracy broadband random spectrometer are achieved by machine learning.
Unsupervised learning methods are used to identify topological variants and non-Hermitian systems based on the given lattice modes distribution.

Now let’s try to answer the three questions at the begining.
First, I think AI methods have several advantages compared to tradition methods, it allows high speed response and can be applied to many different problems without knowing the details. What’s, our experiment have their transferabilty which can be used to understand the physics system properties.
Second, our knowledge in physics did help in explain AI models for example the nonlocal feature of speckle patterns help illustrate why DNN outperforms U-net in MMF image reconstruction. However, we also should know that the current stage is not enough, we could potential find more examples like this.
Third, applying AI in physics research is still at a very early stage, so there are still several challenges to be overcome. For example, AI models general give inaccurate predictions which are not acceptable in some cases. The model is a black box which is contrary to what we expect to do in physics, i.e., try to explain everything in details. Then the data availablity is still a big trouble because sometimes the simulation simply takes too much time.

Look into the future, there are many things that we can do for the next step.
Since we have shown that AI models can be used to approximate complex photonic structures, it is hence easy to implement an inverse design scheme based on the AI approximation.
What’s more, we need invent more AI methods based on physics principles such as difussion models or simulated annealing.
Perheps in the future physics inspired AI models can achieve general intelligence in a smarter way!
That’s all for today’s presentation.
Thank you for your attention!
7. List of publications

8. Interesting things
- The “concept” figure looks really cool, I saw people taking photos while I showed it. Thanks to Xiugou for helping make it!
- Prof. Wang xiao asked me what do you think about people using chatgpt to help with their homeworks…
- Photo by Rimi.

「真诚赞赏,手留余香」
真诚赞赏,手留余香
使用微信扫描二维码完成支付
